Тербелістер мен толқындар

Кез келген физикалық жү йеде тербелмелі қ озғ алыс пайда болу ү шін оғ ан сырттан энергия беру керек. Мысалы, математикалық маятникті тепе-тең дік кү йінен ауытқ ыту арқ ылы оның потенциал энергиясын арттыру керек. Тербеліс кезінде потенциал энергия кинетикалық энергияғ а, кинетикалық энергия потенциал энергияғ а алма-кезек айналып жү йеде тербеліс пайда болады. Егер айналыстағ ы энергия жылуғ а айналып ысырап болмаса, тербелмелі қ озғ алыс шексіз жү реді, яғ ни тербеліс гармоникалық болады. Тербелістегі энергия ысырап болмайтын жү йені мү лтіксіз (идеальный) жү йе деп атайды.

Егер тербелістегі энергия жылу энергиясына айналып ысырап болмаса электрмагнит тербеліс шексіз ұ зақ қ а созылып тербеліс гармоникалық болады.

Бұ л баяндалғ ан деректерден мынадай қ орытындылар жасауғ а болады:

- тербеліс пайда болу ү шін жү йені тепе-тең дік кү йден шығ ару ү шін оғ ан сырттан энергия беру керек;

- тізбекке берілген энергия бір тү рден екінші тү рге алма-кезек айналып жү йеде тербеліс пайда болады;

- егер тербеліс кезінде айналыстағ ы энергия жылу энергиясына айналып ысырап болмаса, тербелмелі қ озғ алыс шексіз ұ зақ созылып тербеліс гармоникалық тербеліске айналады.

Тербелістің кез келген ортада таралуын толқ ын деп атайды. Оларғ а: дыбыс толқ ындары, сағ ат механизмнің жұ мысы, тізбектегі айнымалы ток, электромагниттік тербелістер жә не т.б. жатады.

Жалпы физика курсында кө бінесе тек бірдей қ айталанып отыратын процестерді қ арастырып, оның негізгі кинематикалық тең деулерін жазатын боламыз.

Периодтық қ озғ алыс деп ә рбір циклі дә лме-дә л кез келген басқ а циклін қ айталап отыратын қ озғ алысты атайды. Бір цикл ұ зақ тығ ын период деп атайды.

Тербелмелі қ озғ алысты ерікті жә не еріксіз деп екіге бө леді. Ерікті қ озғ алыста сыртқ ы кү штің ә серінсіз ө з бетінше қ озғ алыс циклін қ айталап отырады. Мұ ндай тербелістерді еркін тербелістер деп атайды.

Ө з бетінше периодтық қ озғ алыстар жасай алатын немесе тербелетін осы тә різді денелер немесе денелер жү йесін (материалдық нү ктелер жиынтығ ын) тербелмелі жү йелер деп атаймыз.

Тербелістерді зерттеуді біз механикалық жү йелердің ең қ арапайым тү рлері: математикалық маятник, физикалық маятник, серпелі маятник, тербелмелі контурды қ арастырамыз.

Математикалық маятник жә не оның кинематикасы.

Математикалық маятник деп – ауырлық центрі іліну нү ктесінен тө мен болатындай етіп ілінген кез келген денені айтады.

Еркін тербелістерді жасай алатын кез келген системаның орнық ты тепе-тең діік қ алпы болады. Математикалық маятник ү шін бұ л қ алып оның ауырлық центрі мен іліну нү ктесі вертикалдық бойында жә не ауырлық центрі іліну нү ктесінен тө мен орналасатын жағ дайғ а сә йкес келеді.

Егер біз маятникті тепе-тең дік қ алпынан шығ аратын болсақ, онда тепе-тең дік қ алпының оң жағ ына, бір сол жағ ына шығ ып, тербеле бастайды. Маятниктің тепе-тең діктен ең ү лкен ауытқ уын тербелістің амплитудасы деп атайды. Амплитудданың бастапқ ы қ озғ алыс шартына тә уелділік қ асиеті барлық тербелмелі қ озғ алыстарғ а тә н деуге болады.

Тербелмелі қ озғ алыстың периодтылығ ын (ырғ ақ тылығ ын) сипаттайтын Т шамасын тербелістің периоды деп атайды. Тербелістің периодын толық бір тербеліске кеткен уақ ытпен ө лшейді.

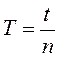(1)

мұ ндағ ы: n- тербеліс саны, t - сол n тербеліске кеткен уақ ыт.

Тербелмелі қ озғ алыстың қ айталанғ ыштық жылдамдығ ын сипаттайтын шаманы оның 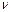жиілігі деп атайды.

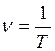(2)

Дене тербелісінің жиілігін бірлік уақ ыттағ ы толық тербелістер санымен ө лшейді.

Ал 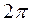секунд ішінде жасалатын тербеліс санын циклдік (дө ң гелек) жиілік (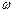, Гц) деп атайды.

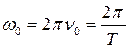(3)

Ә рбір уақ ыт мезетіндегі тербелістегі нү ктенің координата фазасымен (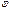, рад, градус) сипатталады.

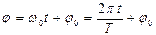(4)

Мұ ндағ ы - бастапқ ы фаза, яғ ни мезеттегі фазаның мә ні.

Тепе-тең діктен ауытқ ытылғ ан математикалық маятникке, жіптің керілу кү ші – Т, ауырлық кү ші P=mg жә не қ алпына келтіруші кү ш F жә не жіптің реакция кү ші N ә сер етеді. (2-cурет)

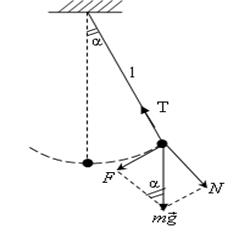
2-сурет

Қ алпына келтіруші кү штің моменті

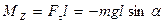(5)

мұ ндағ ы - маятниктің тепе-тең діктен ауытқ ушы бұ рышы, 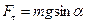- қ алпына келтіруші кү ш, l –маятник жібінің ұ зындығ ы, g – еркін тү су ү деуі, 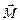мен 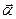ауытқ у (псевекторлар) векторларының бағ ыттары бір-біріне қ арама-қ арсы болғ андық тан (5) тең деуінің алдына «-» таң басы қ ойылады.

Қ атты дененің динамикасының 2-ші заң ы бойынша

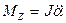(6)

мұ ндағ ы J - маятниктің инерция моменті. Енді (5), (6) тең деулерінен

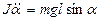(7)

Маятниктің тепе-тең діктен аз ауытқ ығ ан жағ дайы ү шін 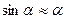жә не 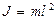тең екендігін ескере отырып (7) тең деуді

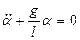(8)

мұ ндағ ы 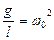деп белгілеп

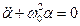(9)

жазып, бұ л тең деуді тербелістің дифференциалдық тең деуімен салыстырсақ, онда математикалық маятниктің гармоникалық тербелісінің

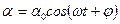(10)

гармоникалық заң ы тү рінде жазуғ а болады.

Сонда

,

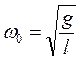ал периоды

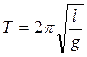(11)

Бұ л тең деу математикалық маятник ү шін жазылғ ан Томсон формуласы деп атайды.

Физикалық маятник. Қ атты дене (3-сурет) ауырлық кү шінің ә серінен горизонталь бағ ытта С масса центрімен сә йкес келмейтін О нү ктесінің маң ында тербелмелі қ озғ алысқ а тү седі. О нү ктесін ілу нү ктесі деп атайды. Қ алпына келтіруші кү штің моменті:

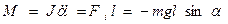
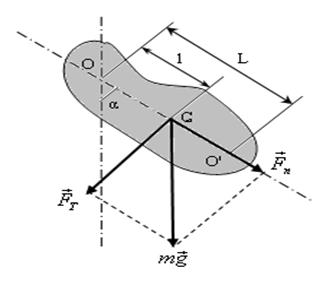
3-cурет

мұ ндағ ы J - ілу нү ктесі арқ ылы ө тетін оське қ атысты инерция моменті, - маятниктен тепе-тең діктен ауытқ у бұ рышы, 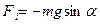- қ алпына келтіруші кү ш, l=OC маятниктің масса центрі мен ілу нү ктесінің аралығ ы.

Динамиканың екінші заң ы бойынша қ алпына келтіруші кү ш ү шін

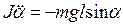
сонда -аз мә ні ү шін

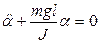
физикалық маятник гармоникалық тербеліс жасайды.

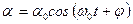
мұ ндағ ы: 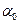- тербелістің циклдік (дө ң гелек) жиілігінің амплитудасы

периоды

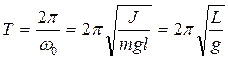(12)

мұ ндағ ы: 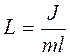- физикалық маятниктің келтірілген ұ зындығ ы деп аталады.

ОС тү зуінің бойында жатқ ан О ілу нү ктесінен келтірілген ұ зындық қ а L тең аралық та жатқ ан О' нү ктесін физикалық маятниктің тербелу центрі деп атайды. Физикалық маятниктің ілу нү ктесі мен тербеліс центрілерін ө зара алмастыруғ а болады. Бұ л жағ дайда физикалық маятниктің тербеліс периоды ө згермейді.

Жоғ арыдағ ы (12) тең деуді физикалық маятник ү шін Томсон формуласы деп атайды.

Серіппелі маятник – абсолютті серпімді серіппеге ілінген массасы m жү йе серпімді кү штің ә серінен тү зу сызық ты гармоникалық қ озғ алыс жасайды (4-сурет)

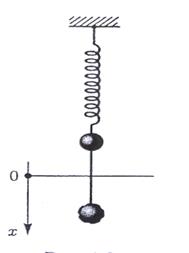
4-сурет

Маятникті қ алпына келтіруші кү ші деформацияланғ ан серіппенің ығ ысу шамасы тура пропорционал болады.

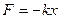
мұ ндағ ы: k - серіппенің қ атаң дығ ы.

Маятниктің қ озғ алыс тең деуі

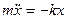
дифференциалдық тең деуі

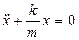немесе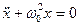

Серпімді кү штің ә серінен ол вертикаль тік бағ ытта гармоникалық тербеліс жасайды.

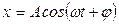
циклдік (дө ң гелек) жиілігі

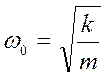
периоды

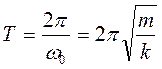(13)

Бұ л (10) тең деуді серіппелі маятник ү шін Томсон формуласы деп атайды.

Тербелістегі нү ктенің берілген уақ ыт мезетіндегі тепе-тең дік қ алпына қ атысты орын сипаттайтын шаманы ығ ысу деп атайды.

Ығ ысуды тербелістегі нү ктенің орнық ты тепе-тең дік қ алпынан оның осы уақ ыт мезетіндегі орнына дейінгі қ ашық тық пен ө лшейді.

А – амплитуда сан мә ні жағ ынан тербелістегі нү ктенің орнық ты тепе-тең дік қ алпынан ең ү лкен 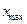ауытқ уына тең шама

Гармоникалық тербелістің тең деуі, жылдамдығ ы, ү деуі жә не энергиясы мен сызбасы (графигі).

Тербелмелі нү ктенің ығ ысуының уақ ытқ а тә уелділігін ө рнектейтін формуланы тербелмелі қ озғ алыстың тең деуі деп атайды. Ол гармоникалық тербеліс тең деуімен сипатталады.

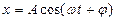(14)

Механикалық гармоникалық тербелістені нү ктенің жылдамдығ ы, ү деуі, энергиясы

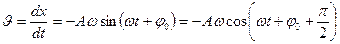(15)

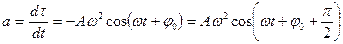(16)

мұ ндағ ы 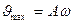, 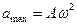-жылдамдық пен ү деу амплитудалары.

Бұ л (15), (16) тең деулерден тербелмелі қ озғ алыстың жылдамдығ ы мен ү деуі, жиілігі х ығ ысу жиілігіндей болатын гармоникалық заң дылық бойынша жү реді. Жылдамдық (14) фазасы, ү деу (15) фазасынан сә йкесті ығ ысу фазасын жә не айырылады (5 – сурет).

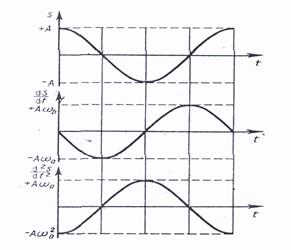
5-сурет

Материалдық нү ктенің гармоникалық тербелісінің кинетикалық энергиясы

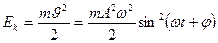(17)

немесе

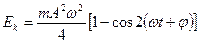(18)

Серпімді 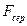кү штің ә серінен гармоникалық тербеліс жасайтын материалдық нү ктенің потенциалдық энергиясы

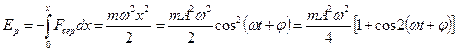(19)

Толық энергия

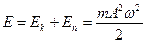(20)

Бұ л (18) жә не (19) тең деулерден кинематикалық энергия мен потенциалдық энергиялардың жиілігі (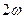), яғ ни гармоникалық тербеліс жиілігінен екі есе кө п болады (6-сурет). Ө йткені 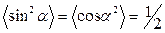, онда (17) жә не (19) тең деулерінен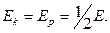

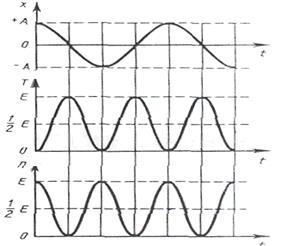
6-сурет

Гармоникалық тербелістерді қ осу.

1. Бағ ыттары мен жиіліктері бірдей гармоникалық тербелістерді қ осу.

Тербелетін денеде бірнеше тербелмелі процестер жү руі мү мкін. Сондық тан осындай тербелістердің қ орытқ ы амплитудасын анық тау керек болады.

Жиіліктері мен бағ ыттары бірдей гармоникалық тербелістерді қ осу ү шін векторлық диаграмма ә дісін қ олданады (7-сурет).

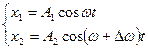
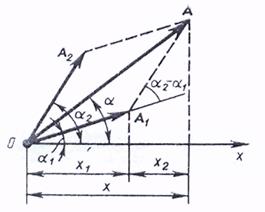
7-сурет

Қ орытқ ы ығ ысу амплитудасы мен бастапқ ы фазасы

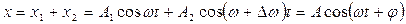(21)

мұ ндағ ы

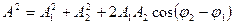(22)

Бастапқ ы фаза

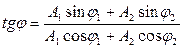(23)

Қ орытқ ы гармоникалық тербелістің амплитудасы фаза айырымына 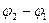тә уелді болады.

Енді (22), (23) тең деулерді талдайтын болсақ, онда

1)

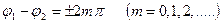
Қ орытқ ы тербелістің амплитудасы жеке тербелістердің амплитудаларының алгебралық қ осындысына тең болады:

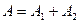
2)

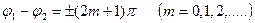
Қ орытқ ы тербелістің амплитудасы жеке тербелістер амплитудасның айырымына тең

.

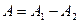Бір бағ ытта тербелетін қ осылатын екі тербелістің жиіліктері бір-бірінен сә л ө згешелеу 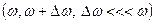. Қ орытқ ы тербелістің амплитудасы периодты тү рде ө згереді, мұ ндай тербелісті соғ у деп атайды.

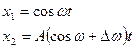
Сонда

()

Мұ ндағ ы 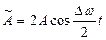соғ у амплитудасы деп, ал 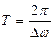соғ у периоды деп атайды.

Ө шетін тербелістер.

Реал (нақ ты) тербеліс жү йесінде кедергі кү ші 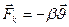ә серінен нү ктенің энергиясы imкi энергияга айналады, соның салдарынан уақ ыт ө туімен бipre оның тербеліс амплитудасы азаяды. Мұ ндай козғ алыс мына дифференциалдық тең деумен сипатталады:

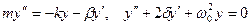
мұ ндағ ы 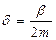- ө шу коэффициенті, 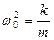- ортаның кедергісі болмағ анда () жү йенің жасайтын еркін тербелістерінің жиілігі.

Тербеліс тең деуі:

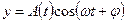
мұ ндағ ы: 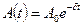- ө шетін тербелістің амплитуда­сы, А_о — бастапкы амплитуда.

Бip-бipiнен периодқ а сә йкес уакытқ а ажыратылатын амплитудалар катынасының логарифмі логарифмдік декремент деп аталады:

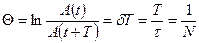
Амплитуда е ~2, 7 есе кемитін 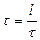(релаксация уақ ыты) уақ ыт ішінде жү йе 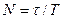тербеліс жасап ү лгереді. Тербелмелі жү йені сипаттау ү шін сапалық (Q) деп аталатын шама енгізеді:

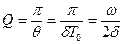
Ө шетін тербелістің периоды мен жиілігі мынағ ан тең:

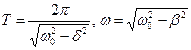
Орта кедергісі аз болғ ан жағ дайда, яғ ни .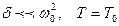

Еріксіз тербелістер деп тербелмелі жү йеде периодты тү рде ө згеретін 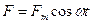кү штің ә серінен пайда болатын ө шпейтін тербелістерді айтады.

Серіппелік маятниктің қ озғ алысының дифференциалдық тең деуі былай жазылады:

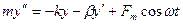
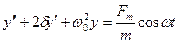
мұ ндағ ы: 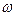-сыртқ ы ә сер ететін кү ш жиілігі. дифференциалдық тең деулер теориясынан біртекті емес тең деудің жалпы шешімі оғ ан сә йкес келетін біртекті тең деудің жалпы шешімі мен біртекті емес тең деудің 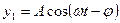дербес шешімінің қ осындысына тең.

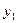() қ осылғ ышы тербелістің орнығ уы деп атайды, ол бастапқ ы кезең де ғ ана роль атқ арып, уақ ыт ө ткен сайын кемиді, оны ескермеуге де болады.

Сонымен (y) функциясы орнық қ ан еріксіз тербелістерді сипаттайды:

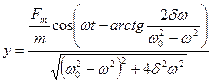
Еріксіз тербелістің амплитудасы мә жбү р теуші кү штің 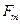амплитудасына пропорционал жә не оның жиілігіне тә уелді:

.

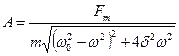Еріксіз тербелістер фазасы бойынша мә жбү р теуші кү штен қ алып қ ояды да, ә рі қ алу шамасы мә жбү р етуші кү ш жиілігі 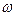-ғ а тә уелді.

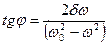
Сыртқ ы кү штің 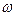жиілігі жү йенің меншікті 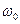жиілігіне жақ ындағ анда еріксіз тербеліс амплитудасының ең ү лкен мә ніне жету қ ұ былысы резонанс деп, ал оғ ан сә йкес келетін жиілік резонанстық жиілік деп аталады.

Механикалық толқ ындар. Серпімді ортада тербелістің таралуын механикалық толқ ын деп атайды. Орта бө лшектерінің тербеліс бағ ыты толқ ынның таралу бағ ытымен бағ ыттас болса, онда толқ ындарды қ ума, ал толқ ынның таралу бағ ытына перпендикуляр бағ ытталғ ан болса, кө лденең толқ ындар деп атайды.

Толқ ын фронты (немесе толқ ындық бет) деп, бірдей фазаларда тербелетін нү ктелердің геометриялық орнын айтамыз. ТОлқ ын фронтының тү ріне байланысты толқ ындар жазық жә не сфералық болып бө лінеді.

Бірдей фазада тербеліп тұ рғ ан екі жақ ын жатқ ан нү ктенің ара-қ ашық тығ ын толқ ын ұ зындығ ы деп атайды:

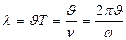
мұ ндағ ы: Т – тербеліс периоды, 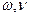-жиілік.

Толқ ын тең деуін жә не оның шешімін мына тү рде жазуғ а болады:

, ,

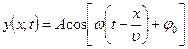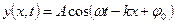
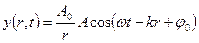
мұ ндағ ы: х – О толқ ындық кө зінен ортаның қ арастырып жатқ ан А нү ктесіне дейінгі арақ ашық тық, 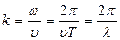- толқ ындық сан, ол 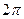– ұ зындық бірлігіне қ анша толқ ын жайғ асатынын кө рсететін сан.

Толқ ын фазасы тұ рақ ты десек, яғ ни 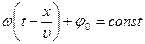, онда фазалық жылдамдық, яғ ни фазаның орын ауыстыру жылдамдығ ы:

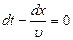, бұ дан .

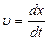(1) ө рнегі х шамасының арту бағ ытында таралатын жазық тық, ал (2) сфералық толқ ынның тең деуінде r – толқ ын кө зінен ортаның қ арастырып отырғ ан нү ктесіне дейінгі ара-қ ашық тық, ал А – толқ ын кө зінен 1-ге тең қ ашығ ы сан жағ ынан амплитудағ а тең тұ рақ ты шама. Қ ума жә не кө лденең толқ ындардың фазалық жылдамдық тары мынағ ан тең:

,

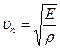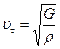
мұ ндағ ы: E, G – Юнг, ығ ысу модульдері, 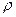-ортаның тығ ыздығ ы.

Негізгі ә дебиеттер:

1. Абдула Ж., Т. Аязбаев. Физика курсының лекциялары. Дә уір, 2012

2. Ақ ылбаев Ж.С., Гладков В.Е., Ильина Л.Ф., Турмухамбетов А.Ж., Механика. Астана, Фалиант баспасы, 2004.

3. Қ ойшыбаев Н., Шарық баев А.О. Физика. Алматы, 2001

Қ осымша ә дебиеттер:

1. Қ ойшыбаев Н. Механика. Алматы, Зият пресс баспасы, 2005

2. Савельев И.В. Жалпы физика курсы. М., Наука, 1986.