Термодинамиканың екінші бастамасы.

Термодинамиканың бірінші бастамасы негізінде қ андай да бір жылу кө зінен алынғ ан жылудың Q мө лшерінің есебінен жұ мыстық зат (газ) А жұ мысын атқ арып отырады.

Пайдалы ә сер коэффициенті 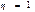болатын жылу қ озғ алтқ ыштары тө тенше тиімді қ озғ алтқ ыш болғ ан болар еді. Ө йткені мұ ндай қ озғ алтқ ыш жасау ү шін қ ыздырғ ыш пен суытқ ыштың болуы шарт емес. Ондай қ озғ алтқ ыштар қ оршағ ан ортадағ ы кез келген денені, мысалы жер қ ыртысыны немесе мұ хитты, айналадағ ы ең суық денелер температураларына тең температураларғ а бейін суыту есебінен жұ мыс жасай алатын болар еді. Мұ ндай қ озғ алтқ ыш екінші ретті (текті) перпетуум мобильді энергияның сақ талу заң ына қ айшы келеді.

Карно циклі бойынша жұ мыс жасайтын жұ мыс денесіне берілген 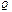жылуы толығ ымен жұ мыс атқ армайды. Суытқ ыш температурасы абсолют нольден жоғ ары (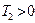) болса, қ ыздырғ ыштың жылуы суытқ ышқ а берілмей қ оймайды.

Кейінерек термодинамиканың екінші бастамасына Клаузиус, Томсон, Планк анық тамалар берді.

Бұ л келтірілген анық тамалардың барлығ ы бір денеден нақ ты жылу мө лшерін алып, ол жылуды толығ ымен жұ мысқ а айналдыратын процесті іске асыруғ а мү мкін емес деген тұ жырымғ а саяды.

Бұ л принцип термодинамиканың екінші бастамасы деп атайды.

Жылу машиналарында жылудың жұ мысқ а айналуы міндетті тү рде қ осымша процеспен, яғ ни 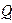жылу мө лшерін суығ ырақ денеге ауыстыру процесімен қ атар жү реді, соның салдарынан ыстығ ырақ денеден алынатын 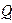жылу мө лшерін толығ ынан жұ мысқ а айналдыру мү мкін емес.

Карно циклінің пайдалы ә сер коэффициенті ү шін жазылғ ан тең деулеріне

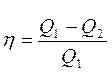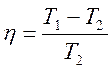, (27)

сү йене отырып

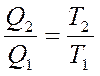немесе 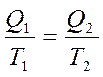(28)

деп жазуғ а болады. Сонда 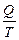-қ атынасты келтірілген жылу мө лшері деп атайды. Карноның қ айтымды циклында жылудың келтірілген мө лшерінің қ осындысы нольге тең болады:

(29)

Бірақ Карноның кез келген циклында п.ә.к. мынадай тең сіздікті қ анағ аттандырады:

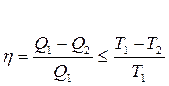(30)

мұ ндағ ы «=» таң басы қ айтымды процесс ү шін орындалады.

Сондық тан Карноның кез келген циклында жылудың келтірілен мө лшерінің қ осындысы нө лден артық бола алмайды. Бұ л тең сіздік 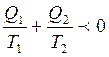Клаузиус тең сіздігі деп аталады.

Кө пшілік жағ дайда келтірілген жылу мө лшерін процестің белгілі бір бө лігінде нақ ты есептеу мақ сатында оны элементар бө ліктерге (5-*сурет) бө леді. Элементар цикл ү шін Клаузиус тең сіздігі:

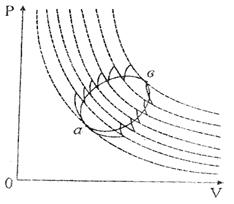
5-сурет

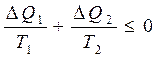(31)

Сонда жалпы толық цикл ү шін бұ л тең сіздікті:

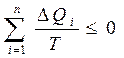(32)

Бұ л қ осынды шекті жағ дайда тұ йық контур бойынша алынғ ан интегралғ а тең:

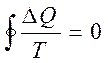(33)

Кез келген қ айтымды тұ йық емес процесте 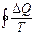шамасының процесс жү ріп ө ткен жолғ а тә уелді болмайтындығ ын кө рсетеді. Ол жү йенің бастапқ ы жә не соң ғ ы кү йлеріне ғ ана тә уелді. Бұ дан дененің жү йенің кү йімен сипаттамасы қ андай да бір S шамасы болады. Сондық тан жү йенің А кү йін сипаттайтын шаманы S_A деп, ал В кү йіне сә йкес келетін шамасын S_B деп белгілейік, қ айтымды процесте S_B-S_A айырымы

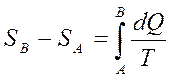(34)

Яғ ни бұ л айырым А жә не В кү йлердің арасында ө тетін қ айтымды процесте жылудың келтірілген мө лшерінің қ осындысына тең болады.

Қ орытындысында қ айтымды процесс ү шін элементар жылудың келтірілген мө лшері 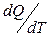жү йенің S функциясының толық дифференциалы болып табылады. Бұ л S функциясы 1866 жылы Р.Клаузиус енгізіп, оны энтропия деп атады.

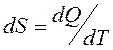(35)

немесе 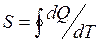(36)

Осы (36) тең деуге сә йкес ішкі энергия мен энтропия ө згерісін қ айтымды процесс ү шін мынадай тү рде жазуғ а болады:

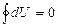(37)

(38)

Сонымен ішкі энергия сияқ ты энтропияда P, V, T параметрлерінің функциясы болып табылады:

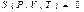(39)

Ал кез келген изопроцестер ү шін (39) тең деуді

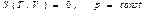(изобаралық процесс)

(изохоралық процесс)

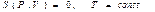(изотермиялық процесс)

Энтропия тұ рақ ты жағ дайда ө тетін процессті изоэнтропиялық процесс деп атайды. Оғ ан адиабаталық процесті жатқ ызуғ а болады. Жоғ арыдағ ы (39) ө рнектен

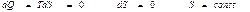(40)

Жоғ арыда жазылғ ан (39) жә не (40) тең деулерге сү йене отырып, ә р тү рлі изопроцестерге сә йкесті энтропияны есептеуге болады.

Идеал газ ү шін 1 кү йден 2 кү йге ө ткен кездегі оның энтропия ө згерісі

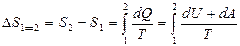(41)

мұ ндағ ы , , .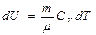

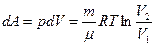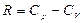еске алсақ, онда

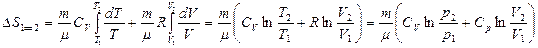(42)

Идеал газда ө тетін процестер кезіндегі энтропия ө згерісі

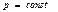
Изохоралық	Изобаралық	Изотермиялық	Адиабаталық

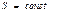
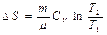
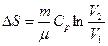
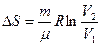
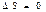
Энтропия:

1) Ө з еркімен жү ретін қ айтымды процестерде тұ йық жү йенің энтропиясы тұ рақ ты кү йінде қ алады.

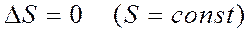
2) Қ айтымды процесc кезінде процеске қ атысатын денелердің ө згерістерінің алгебралық қ осындысы нольге тең болады:

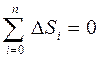
3) Қ айталанбайтын процестерде тұ йық жү йенің энтропиясы міндетті тү рде ө седі:

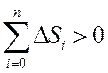
Бұ л тең сіздік қ айтымды процеске қ атысушы барлық денелердің энтропиялары ө згерістерінің алгебралық қ осындысы ә рқ ашанда нольден ү лкен болады. Клаузиус енгізген бұ л тең сіздік энтропияның ө су принципі деп аталады.

Бұ л жерде жү йеге енетін денелердің энтропиялары бірдей ө седі деген ой тумауы керек. Ө йткені жү йеге бірігетін денелердің энтропиясы азайса, ал екіншісінікінің ө суімен жойылып отырады да, жалпы процес кезінде энтропия ө суі байқ алады. Мысалы газды изотермиялық жағ дайда сық қ анда, оның энтропиясы азаяды. Бірақ термостаттың энтропиясы ө седі (термостат жылу алады).

Сонымен қ айтымды жә не қ айтымсыз процестер ү шін термодинамиканың екінші бастамасы:

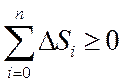
Табиғ атта кездесетін процестер қ айтымсыз процестер болатындық тан, оқ шауланғ ан жү йелерде энтропияның ө суіне ә келетін процестер жү реді.

Термодинамикалық потенциалдар.

Термодинамикадлық есептерде термодинамикалық потенциалдар деп аталатын кү й функцияларын пайдалануғ а болады. Тә уелсіз параметрлердің ә рбір жиынтық тарына термодинамикалық потенциалдар сә йкес келеді.

Термодинамикалық потенциалды қ арастырғ ан кезде

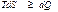(43)

қ атынасын пайдаланады. Мұ ндағ ы тең дік белгісі (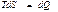) қ айтымды, ал тең сіздік 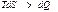қ айтымсыз процестерге жатады.

Ішкі энергия. Термодинамиканың бірінші бастамасын қ айтымды процесс ү шін

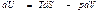(44)

деп жазуғ а болады. Мұ нда U потенциалы ү шін айнымалылар S жә не V болып табылады. Олай болса,

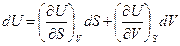(45)

Осы (45) ө рнекті (44) тең деумен салыстырсақ, онда

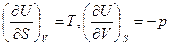(46)

Адиабаталық процесс ү шін сыртқ ы кү штерге қ арсы атқ арылатын жұ мыс

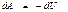
немесе

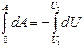
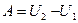(47)

Сонда тұ рақ ты кө лемдегі жылусыйымдылық

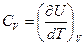(48)

Еркін энергия. Жоғ арыдағ ы (44) тең деу тү рінде жазылғ ан термодинамиканың бірінші бастамасындағ ы атқ арылғ ан жұ мысты

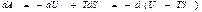(49)

деп жазуғ а болады. Сонда еркін энергия

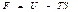(50)

дененің кү й функциясы деп атайды.

Сонда (49), (50) тең деулерге сә йкес қ айтымды изотермиялық процесс кезінде атқ арылатын жұ мыс дененің еркін энергиясының ө знерісіне тең болады:

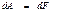(51)

немесе

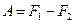(52)

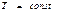( қ айтымды)

Енді (47) тең деумен (52) тең деуді салыстырсақ, изотермиялық процесс кезінде ішкі энергия еркін энергияның адиабаталық процесс кезінде тә різді роль атқ аратынын кө реміз.

Қ арастырғ ан (47) тең деу қ айтымды жә не қ айтымсыз процестер ү шін оырндалады. Ал (10) тең деу тек қ айтымды процесс ү шін орындалады.

Қ айтымсыз процесс ү шін еркін энергия

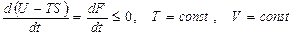(53)

мұ ндағ ы: t - уақ ыт. Бұ л (53) тең деуден (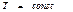) тұ рақ ты температура мен 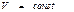тұ рақ ты кө лемде ө тетін процестерде процесс еркін энергияның тө мендеуі есебінен іске асырылады. Жү йе тепе-тең дікке келген уақ ытта F ө зінің уақ ыт бойынша ө згертуін тоқ татады. Яғ ни T мен V шамалары тұ рақ ты болғ ан кезде тепе-тең дік кү й еркін энергияның аз мә ніне сә йкес келетін кү й болып табылады.

Энтальпия. Егер процесс тұ рақ ты қ ысымда ө тетін болса, онда дененің алатын жылуын

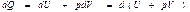(54)

H=U+pV (55)

Н- кү й функциясын энтальпия немесе жылу функциясы деп атайды.

Сонда (49) жә не (55) тең деулер дененің изобаралық процесс кезінде алатын жылу мө лшерін

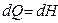(56)

немесе интегралдық тү рде

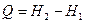(57)

болатындығ ын кө реміз. Демек, қ ысым тұ рақ ты болғ ан кезде дененің алатын жылуы энтальпияның ө сімшесіне тең болады.

Тұ рақ ты қ ысым кезіндегі энтальпия тұ рақ ты кө лем кезіндегі ішкі энергия ролін атқ арады.

Негізгі ә дебиеттер:

1. Ә лжанов К.К., Қ ұ саинов К.К., Мү сенов К.Қ., Дә рібеков С. Молекулалық физика. Қ арағ анды. Қ арМУ.2003

2. Қ ұ лбекұ лы М. Молекулалық физика жә не термодинамика. Алматы, Қ арасай баспасы. 2005

3. Қ ойшыбаев Н. Молекулалық физика. Алматы, Зият пресс баспасы. 2005

Қ осымша ә дебиеттер:

1. Қ ойшыбаев Н., Шарық баев А.О. Физика. Алматы. 2001

2. Савельев И.В. Жалпы физика курсы. М., Наука, 1986.

3. Дә рібеков С. Материалдар физикасының негіздері. Қ арМУ 2005.