
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дәріс 4
|
|
Тақ ырыбы: Молекулалық физика жә не термодинамика
Дә ріс жоспары:
1. Идеал газ.
2. Газ заң дары.
3. Газдардың молекулалық -кинетикалық теориясының негізгі қ ағ идалары.
Дә ріс мә тіні:
Молекулалық физиканың негізіне заттың молекулалық қ ұ рылысы туралы болжам алынады. Бұ л гипотеза бойынша зат ү здіксіз жә не шексіз бө лінбейді. Заттың барлық қ асиетін сақ тайтынең кішкентай бө лшегін молекула деп атайды. Молекулалардың қ озғ алысы кө зге кө рінбейді.
Зат қ ұ рылысының алғ ашқ ы элементтеріне: зат мө лшері, мольдік масса, Авогадро саны сияқ ты ұ ғ ымдар біріктіріледі.
Зат мө лшері – заттың белгілі массасындағ ы қ ұ рылымдық элементтері санымен сипатталады. Қ ұ рылымдық, элементтеріне атомдар, молекулалар, иондар жө не т.б. бө лшектер немесе арнайы бө лшектер тобы жатуы мү мкін. СИ жү йесіндегі зат мө лшерінің ө лшем бірлігі моль деп аталады. Мольдер саны 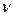 (ню) символымен белгіленеді.
(ню) символымен белгіленеді.
Массасы 0, 012 кг 12С кө міртегі изотопында қ анша атом болса, сонша қ ұ рылымдық элементтеріне ие жү йедегі заттың мө лшері мольге тең деп алынады. Сондық тан, анық тамасы бойынша кез келген заттың бірлік мө лшерінде (бір мольде) қ ұ рылымдық элементтер саны бірдей. Осы санды Авогадро тұ рақ тысы немесе Авогадро саны деп атайды. Бұ л тұ рақ ты итальян ғ алымы А.Авогадро қ ұ рметіне аталғ ан, белгісі 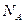 Авогадро тұ рақ тысы іргелі физикалық тұ рақ тылар қ атарына кіреді. Оның мә ні
Авогадро тұ рақ тысы іргелі физикалық тұ рақ тылар қ атарына кіреді. Оның мә ні
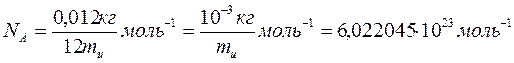 (1)
(1)
Мольді ө ндіретін эталон болмайды, молекулалық шамалар ө лшенбейді, олар есептеледі. Осы (1)-ші ө рнектен мынадай анық тама шығ ады:
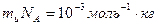 (2)
(2)
Заттың бір молінің массасын мольдік масса деп атайды. Мольдік массаны М ә рпімен белгілейді. (1)-ші формуланы қ олданып, мольдік масса бір молекуланың массасы мен Авогадро санының кө бейтіндісіне тең болатындығ ын кө реміз:
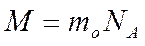 (3)
(3)
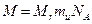 (4)
(4)
Егер газдың N молекуласы болса, онда мольдер саны 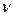 былай табылады:
былай табылады:
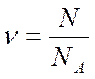 (5)
(5)
Осы тең деуді молекула массасына кө бейтіп, массасы 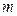 заттың мольдер саны
заттың мольдер саны
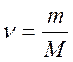 (6)
(6)
екендігін байқ аймыз, осыдан
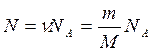 (7)
(7)
болады.
Мұ ндай есептеулер жү ргізгенде элементтердің салыстырмалы атомдық массасы Менделеевтің элементтер периодтық жү йесінен алынады.
Молекулалық физика мен термодинамикада негізінен: идеал жә не реал газ деп аталатын екі физикалық модельдер қ олданылады.
Идеал газ:
– жеке молекуланың кө лемі газ қ ұ йылғ ан ыдыс кө леміне қ арағ анда ескерусіз;
– газ молекулаларының арасында ө зара ә серлесу кү ші болмайды;
– газ молекулалары бір-бірімен жә не ыдыс қ абырғ асымен абсолютті серпімді соқ тығ ысады.
Бұ л модельді қ алыпты жағ дайдағ ы немесе ө те тө менгі қ ысыммен жоғ арғ ы температурадағ ы реал газдар ү шін де қ олдануғ а болады.
Термодинамика немесе жылудың жалпы теориясы аксиоматикалық ғ ылым болып табылады. Ол заттың қ ұ рылымы жә не жылудың физикалық табиғ аты жайлы ешқ андай арнаулы гипотезаларды да, нақ ты кө зқ арастарды да пайдаланбайды. Оның қ орытындылары тә жірибе деректерін жалпылауғ а негізделген принциптер мен болжамдарғ а сү йенеді. Ол жылуды қ андай да бір ішкі қ озғ алыстардың жиынтығ ы деп қ арастырады. Оның қ андай қ озғ алыс екендігінде шаруасы болмайды. Сондық тан молекулалық физиканы зат қ ұ рылымының молекулалық -кинетикалық теориясы (МКТ) деп атайды.
Термодинамикада макроскопиялық жү йелердің кү йлерін зерттеу ү шін термодинамикалық жә не статистикалық ә дістер деп аталатын екі зерттеу ә дістері қ олданылады.
Термодинамикалық ә діс заттың атомдық -молекулалық қ ұ рылымы туралы ешқ андаймодельді кө зқ арастарғ а сү йенбейді жә не ө зінің мә ні бойынша феноменологтық (гректің рһ аnоmеnоn - кө рінетін, білінетін) болады. Термодинамикалық ә дістің міндеті - тікелей тә жірибеде бақ ылайтын шамалардың (қ ысым, температура, кө лем, концентрация жә не т.б.) арасындағ ы байланысты тағ айындау. Кез келген физикалық мә селедерді шешу кезінде термодинамикалық ә дісті колданғ анда, онда заттың атомдық -молекулалық қ ұ рылымымен байланысты ешқ андай шамалар (атом мен молекула ө лшемдері, олардың массасы жә не т.б.) қ арастырылмайды.
Термодинамиканың жалпылығ ы ерекше, оны қ арапайым механизмдер мен адам организмін зерттеуге де қ олдануғ а болады. Бұ дан басқ а, осы теорияның шең берінде ө зіміздің кү нделікті ө мірдегі тә жірибенің біразын тү сінуге болады. Неге кеседегі ыстық шай суиды? Неге ә тірдің иісі барлық бө лмеге таралады деген сияқ ты.
Термодинамикалық ә дістің кү ші, оның ә р тү рлі заттың тікелей байқ алатын қ асиеттерінің арасындағ ы қ атынастарды, олардың ішкі қ ұ рылымы туралы ештең е білмей-ақ тағ айындауда білінеді. Орасан зор сан молекулалардан қ ұ ралғ ан кү рделі жү йелер туралы мә ліметті, тек қ ана тө рттен артық емес, негізгі термодинамикалық заң дар мен бірнеше айнымалы шамаларғ а сү йеніп алуғ а болады. Термодинамиканың тағ ы да бір артық шылығ ы, оның қ орытындылары қ арастырып отырғ ан жү йенің ө згешелігіне тә уелді емес. Мысалы, біз тастың температурасы деп, немесе жә ндіктің, немесе адамның қ олының температурасы жайында пікір айта аламыз. Тас, жә ндіктің денесі, адамның қ олы жылулық тепе-тең дікте болатын қ асиетке ие. Заттың арнайы табиғ и ерекшелігі теорияда бірнеше параметрлер арқ ылы белгіленеді, мысалы жылусыйымдылық, мольдік кө лем деген сияқ ты. Осы ә діс негізінде екі ә р тү рлі кү йдегі жү йелердің қ асиеттері туралы мә ліметтер алуғ а мү мкіндік шығ ады.
Тепе-тең дік термодинамикасы жү йені тыныштық кү йінде бейнелейді, оны кө рнекі тү рде былай сипаттауғ а болады " осында жә не қ азір", ол жү йенің бұ рынғ ы жайтын жә не алғ ашқ ы кү йден соң ғ ы кү йге ө ту жолын ескермейді.
Статистикалық ә діс термодинамикалық ә діске қ арама-қ арсы, ол бастан макроскоптық жү йелердің қ асиеттерін зерттегенде модельдік атомдық -молекулалық кө зқ арастарғ а негізделген. Статистикалық ә дістің мақ сатын былай тұ жырымдауғ а болады: заттың макроскоптық мө лшерінің қ асиеттерінің ө згерісі заң ын тағ айындау ү шін, оның қ ұ рамындағ ы бө лшектердің (молекула, атом, ион жә не т.б.) қ озғ алыс заң дарын білу қ ажет. Сондық тан статистикалық физика термодинамика заң дарының теориялық дә лелдеуін атомдық -молекулалық тұ рғ ыдан кө рсетеді.
Жалпы жағ дайда осы екі ә діс бір-біріне ұ штасып, бірлестірілген статистикалық термодинамика ә дісін қ ұ растырады.
Молекулалық физиканың дамуының ө те маң ызды кезең і кинетикалық теориямен байланысты. Кинетикалық деген ұ ғ ым қ озғ алысқ а қ атысы бар дегенді білдіреді, сондық тан қ ұ былыстарды зерттеу ү шін, олардың динамикалық сипаттарғ а қ атысты екенін кө рсетеді. Жылудың кинетикалық теориясы бойынша молекулалар шапшаң немесе баяу қ озғ алады, егер олар қ ұ рамына кіретін дене ыстығ ырақ немесе суығ ырақ болса. Жылулық энергиясы дененің шындығ ында оның қ ұ рамындағ ы кө зге кө рінбейтін молекулалық қ озғ алыстың денеге қ атысты тұ тас механикалық (кинетикалық жә не потенциалдық) энергиясы болып келеді. Осы тү сінік бойынша жылулық энергия қ ұ рамына молекулалардың ілгерілемелі қ озғ алысының кинетикалық энергиясы жә не молекула қ ұ рылымындағ ы атомдардың айналмалы кинетикалық энергиясы мен тербелісінің кинетикалық жә не потенциалдық энергиясы кіреді. Осыдан, “молекулалардың жылулық қ озғ алысы” деген термин (латынның terminus - ғ ылымда қ олданатын белгілі ұ ғ ымды дә л белгілейтін сө з) шығ ады.
Молекулалық гипотеза мен жылулық кинетикалық теориясы заттың кез келген кү йіне қ олданылады. Заттың ү ш агрегаттық (латынның aggrego - қ осыламын) кү йлері – қ атты, сұ йық жә не газ тә різдес молекулалардың жақ ындық дә режесі мен қ озғ алыстарының қ арқ ындылығ ымен айырылады. Қ атты денеде бө лшектер бір-бірімен тығ ыз жанасады, сондық тан ө те сирек жағ дайда олардың кейбіреуі кө ршілері арасымен сырғ анап орын ауыстыруы мү мкін. Қ атты денені қ ыздырғ анда молекулалар қ озғ алысы ү дейді, ол дененің жылулық ұ лғ аюына ә келеді. Бір мезгілде сыртқ ы қ ысымғ а байланысты бір-біріне тығ ыз жабысқ ан молекулағ а бір топтан екінші топқ а ауысуына мү мкіншілік туады. Осы жағ дай заттың сұ йық кү йгеауысуына мү мкіндік береді, одан арғ ы қ ыздыру молекулалардың ө зара байланыс кү шін ү зіп, оларғ а еркін қ озғ алуғ а мү мкіншілік туғ ызады, сондық тан молекулалар кез келген қ олайлы кең істікті жайлайды; зат газ тә різдес кү йге ауысады.
Қ ысым мен температураның бір мә ндерінде заттың екі фазасы (сұ йық пен газ, қ атты мен сұ йық немесе қ атты мен газ тә різдес) бірге қ атар тепе-тең дік кү йде бола, ө мір сү ре бастайды. Тек бір белгілі қ ысым мен температура мә нінде заттың барлық ү ш фазасы бірте тепе-тең дік кү йде катар ө мір сү ре алады. Кү й диаграммасындағ ы осы нү ктені ү штік нү кте деп атайды.
Газдың тығ ыздығ ы сұ йық немесе қ атты кү йдегі заттың тығ ыздығ ымен салыстырғ анда кіші болады. Сондық тан газдың молекулаларының арақ ашық тығ ы, олардың ө лшемдерінен ә лдеқ айда ү лкен. Қ озғ алыстағ ы молекулалар бір-біріне ә лсіз ә сер етеді, тек жакындасқ анда жолдары алғ ашқ ы бағ ыттарынан елеулі ауытқ уы мү мкін. Бұ л жағ дайда молекулалар бір-бірімен соқ тығ ысты дейді.
Сонымен, молекула-кинетикалық теория заттың кү йлерін жә не ондағ ы байқ алатын қ ұ былыстарды молекулалар арасында ә сер ететін кү штермен байланыстырады. Молекулааралық кү штердің табиғ аты эксперименттік зерттеулер мен теориялық болжаулар нә тижесі арқ ылы айқ ындалады. Мысалы, газдардың сұ йық қ а айналуы, ү лкен қ ашық тық тарда молекулалар арасында тартылыс кү штері, ал сұ йық тың сығ ылуғ а қ атты карсылығ ы, жақ ын қ ашық тық та тебу кү штері болатынын дә лелдейді жә не қ ашық тық қ а қ атысты бұ л кү штер қ атты ө згереді.
Молекулааралық кү штерді жақ ыннан ә рекеттесу жә не алыстан ә рекеттесу деген екі топқ а бө леді. Жақ ыннан ә рекеттесу кү штерін валенттік кү штер немесе химиялық кү штер деп те атайды. Молекулалар соншалық ты жақ ындасқ анда, тіпті олардың сыртқ ы электрондық бұ лттары бү ркелген кезде, тебу кү штері пайда болады. Молекулалық ө лшемдерінен ү лкен қ ашық тық та молекулалар бірін-бірі тарта бастайды, демек тартылыс кү штер пайда болады.
Молекулалық физика мен термодинамикада ө те кө п молекулалардан тұ ратын жү йе қ асиеттері зерттеледі.
Термодинамикалық жү йе деп ө зара жә не сыртқ ы қ оршағ ан ортамен энергия жә не масса алмасуғ а қ абілетті денені немесе денелер жиынтығ ын айтады.
Кез келген материялық дене орасан кө п микробө лшектерден жә не молекулалардың ү лкен жиынтығ ынан тұ рады. Мұ ндай денелерді макроскоптық жү йе дейді. Макроскоптық жү йелердің ө лшемдері ә рқ ашан да атом мен молекула ө лшемдерінен едә уір ү лкен.
Термодинамикалық жү йені сипаттайтын барлық макроскоптық белгілерін макроскоптық параметрлер деп атайды. Оларғ а, мысалы тығ ыздық, кө лем, қ ысым, концентрация жә не т.б. жатады.
Макроскоптық параметрлер сыртқ ы жә не ішкі болып бө лінеді. Қ арастырып отырғ ан жү йеге кірмейтін сырттағ ы денелердің макро- сипаттары сыртқ ы параметрлерге жатады.
Термодинамикалық жү йенің кү йін тә уелсіз макроскоптық параметрлер жиынтығ ы анық тайды. Жү йенің бұ рынғ ы ө ткен жайттарына тә уелсіз жә не тап осы кездегі кү йін толық анық тайтын шамаларды кү й функциялары дейді.
Егер жү йенің параметрлері уақ ыт бойынша ө згермесе, оның кү йін
стационарлық деп атайды.
Сонымен, жү йенің термодинамикалық кү йін, оның барлық қ асиеттерінің жиынтығ ы анық тайды.
Термодинамикалық жү йе деп термодинамикалық тепе-тең дік кү йде болатын макрожү йелерді айтады. Тепе-тең дік кү йдегі жү йені сипаттайтын шамаларды P, V, T термодинамикалық параметрлер деп атайды.
Жү йенің бір кү йден екінші кү йге ө туі, жү йенің тепе-тең дік кү йден шығ уымен байланысты болады. Демек, жү йе қ андай да бір жү рген кезде тепе-тең дік емес кү йлерінің тізбегінен ө теді.
Тепе-тең дік кү йлердің ү здіксіз тізбегінен қ ұ рылғ ан тепе-тең дік деп аталады. Тепе-тең дік кезінде жү йенің барлық макропараметрлері ө те баяу, физикалық шектеусіз баяу, болымсыз ө згереді, ә р тү рлі нү ктелеріндегі параметрлердің мә ні, мысалы қ ысым болса, қ айсыбір орташа 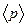 мә ніне жақ ын болады. Бұ л айтылғ андардан, тек шектеусіз баяу ө тетін тепе-тең дік бола алады.
мә ніне жақ ын болады. Бұ л айтылғ андардан, тек шектеусіз баяу ө тетін тепе-тең дік бола алады.
Егер тепе-тең дік кү йінен жү йе шығ арылып жә не еркіне жіберілсе, онда ол біраз уакыттан кейін қ айтадан тепе-тең дік кү йіне оралады. Жү йенің тепе-тең діксіз кү йінен тепе-тең дік кү йіне ө ту процесі релаксация деп аталады, aл жү йенің тепе-тең дік кү йге оралу уақ ытын релаксация уақ ыты дейді.
Термодинамикалық жү йеде ө тетін процестің жылдамдығ ы релаксация жылдамдығ ынан едә уір кіші делік, онда бұ л процестің кез келген кезең інде барлық параметрлер мә ндері тең еліп ү лгереді. Сондық тан мұ ндай бір-біріне шексіз жақ ын тепе-тең дік кү йлердің тізбегінен тұ рады. Осындай жеткілікті баяу процестерді квазистатикалық немесе тепе-тең дік деп те атайды.
Жү йелердің кү йлері мен процестерін бейнелеу ү шін графиктік ә дісті қ олданады. Біртекті жү йе кү йлері нү ктелермен белгіленеді, ал процестерді 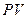 ,
, 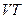 жә не т.б. жазық та сә йкес сызық тар бейнелейді. Айта кету керек, тек қ ана тепе-тең дік кү йлер мен процестерді графиктік бейнелеу мү мкін. Осындай да тепе-тең дік кү й ә р мезетте макропараметлердің белгілі бір мә німен сипатталатын болады.
жә не т.б. жазық та сә йкес сызық тар бейнелейді. Айта кету керек, тек қ ана тепе-тең дік кү йлер мен процестерді графиктік бейнелеу мү мкін. Осындай да тепе-тең дік кү й ә р мезетте макропараметлердің белгілі бір мә німен сипатталатын болады.
Тепе-тең дік кү й жә не тепе-тең дік ұ ғ ымдары молекулалық физикада маң ызды орын алады.
Ә рине, барлық нақ ты процестер тепе-тең діксіз, сондық тан олар тепе-тең дік кү йге белгілі дә режеде жуық тауы мү мкін. Сондық тан тепе-тең дік процесі уақ ыт бойынша қ айтымды. Жү йе тура бағ ытта кандай кү йлерден ө тсе, кері процесте сондай кү йлер тізбегінен ө туі қ ажет. Осындай тепе-тең дік процестерді қ айтымды теп атайды. Мысалы, жү йе ABC ө згерістерге ұ шырады делік (1- сурет). Бұ л ө згерістер қ айтымды болады:
а) егер кері СВА бағ ыттағ ы ө згерістер сондай алдындағ ы тура бағ ыттағ ы мә ндеріне сә йкес келсе;
б) қ оршағ ан ортамен не жылу, не затпен алмасып жә не жұ мыс ө ндірсе, онда кері бағ ыттағ ы процестің СВА бө ліктерінде сондай мө лшерде жү йе жылу шығ арады да, жұ мыс орындалады. Мысаяы, ABC жолында жү йе 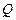 жылу мө лшерін алды делік, онда кері СВА-мен қ айтқ анда, ол тура сондай
жылу мө лшерін алды делік, онда кері СВА-мен қ айтқ анда, ол тура сондай 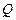 мө лшерде жылуды шығ аруы қ ажет.
мө лшерде жылуды шығ аруы қ ажет.

1 - сурет
Осы екі шарттарды қ анағ аттандырмайтын ө згерістердің барлығ ы қ айтымсыз процестер деп аталады. Табиғ атта ө тетін барлық процестер қ айтымсыз.
Тығ ыздық
Термодинамикалық жү йенің 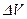 кө леміндегі қ асиетінің мө лшерін
кө леміндегі қ асиетінің мө лшерін 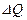 деп белгілейік.
деп белгілейік. 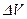 кө лемдегі қ асиеттің
кө лемдегі қ асиеттің 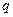 тығ ыздығ ын
тығ ыздығ ын 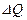 мө лшерін осы кө лемнің
мө лшерін осы кө лемнің 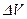 шамасына қ атынасы тү рінде анық тайды:
шамасына қ атынасы тү рінде анық тайды:
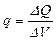 . (8)
. (8)
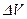 жү йенің толық V кө лемінің бө лігі, сондық тан қ асиеттің мө лшерін (8) ө рнекті интегралдау арқ ылы табамыз:
жү йенің толық V кө лемінің бө лігі, сондық тан қ асиеттің мө лшерін (8) ө рнекті интегралдау арқ ылы табамыз:
 , (9)
, (9)
мұ ндағ ы dV – жү йенің шексіз кішкене бө лігінің кө лемі.
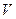 кө лемдегі газ массасы
кө лемдегі газ массасы 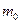 біркелкі молекуладан қ ұ ралғ ан делік. Молекулалар саны N. Онда (6) ө рнегін қ олданып, газдың
біркелкі молекуладан қ ұ ралғ ан делік. Молекулалар саны N. Онда (6) ө рнегін қ олданып, газдың 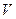 кө леміндегі массасын былай табамьз:
кө леміндегі массасын былай табамьз:
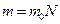 . (10)
. (10)
Бірлік кө лемдегі газдың массасының тығ ыздығ ын 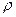 деп белгілейді. Онда (8) жә не (10) ө рнектерге сү йеніп,
деп белгілейді. Онда (8) жә не (10) ө рнектерге сү йеніп,
 (11)
(11)
деп жаза аламыз.
Бірлік кө лемдегі молекулалар саны немесе сандық тығ ыздығ ы (8) бойынша мынағ ан тең болады:
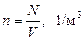 (12)
(12)
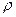 жә не
жә не 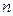 байланысты, оны (10) жә не (11) ө рнектерін ескеріп, анық таймыз:
байланысты, оны (10) жә не (11) ө рнектерін ескеріп, анық таймыз:
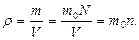 (13)
(13)
Осыдан, массалық тығ ыздық бір молекула массасын сандық тығ ыздық қ а кө бейту арқ ылы анық талады жә не ол бірлік кө лемдегі молекулалар санына тура пропорционал болады. Егер заттың 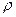 тығ ыздығ ы белгілі болса, онда (9) формула бойынша барлық
тығ ыздығ ы белгілі болса, онда (9) формула бойынша барлық 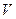 кө лемдегі оның толық массасы
кө лемдегі оның толық массасы
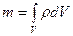 (14)
(14)
болатындығ ы анық.
Егер заттың қ асиеті оның бірлік массасына қ атысты анық талса, онда оны меншікті қ асиет деп атайды. Мысалы, меншікті кө лем 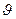 тө мендегі ө рнек арқ ылы табылады:
тө мендегі ө рнек арқ ылы табылады:
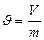 (15)
(15)
мұ ндағ ы 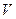 – газдың кө лемі,
– газдың кө лемі, 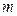 –газдың массасы.
–газдың массасы.
(11) ескерсек, онда меншікті кө лем 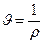 тығ ыздық қ а керіпропорционал болады.
тығ ыздық қ а керіпропорционал болады.
Заттың бір моліндегі қ асиеті мольдік деп аталады. Мысалы, мольдік масса немесе мольдік кө лем. Температурасы мен қ ысымы бірдей идеал газдардың мольдік кө лемдері бірдей болады. Мысалы, қ алыпты жағ дайда, температура 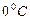 жә не қ ысымы 760 мм сын.бағ. болғ анда, бір моль идеал газдың кө лемі
жә не қ ысымы 760 мм сын.бағ. болғ анда, бір моль идеал газдың кө лемі 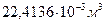 болады.
болады.
Концентрация
Жалпы жағ дайда кез келген агрегаттық кү йде бір зат екінші заттың ортасында немесе бірнеше заттардың ішінде бірқ алыпты бө лініп таралуы мү мкін. Мұ ндай заттың араласуына газдар қ оспасы, сұ йық тар ерітіндісі, қ атты денелер ерітіндісі (қ орытпалар) жә не аралас кристалдар жатады.
Бірнеше заттың араласуын бір заттың молекулаларының екіншісінің ішінде қ арапайым таралуы ден тү сінуге болмайды, негізінде мұ ндай араласу ә р тү рлі молекулааралық ә рекеттесулерге байланысты болады.
Қ оспа (ерітінді, қ орытпа) қ ұ рамындағ ы затты компонент (латынның соmponens - қ ұ раушысы) деп атайды. Қ оспаның қ осылыс сандық қ ұ рамын ә р тү рлі тә сілдер арқ ылы анық тайды. Қ оспаның бірлік массасындағ ы немесе бірлік кө леміндегі зат компоненттерінің мө лшерін концентрация деп атайды. Концентрация ә детте, қ оспаның компоненттерінің салыстырмалы мө лшерін сипаттайтын шама болады. Сондық тан, ол процентпен немесе компоненттің массалық немесе мольдік ү лесімен анық талуы мү мкін.
Қ оспадағ ы заттың физикалық қ асиеттері компоненттердің қ асиеттерімен тығ ыз байланысты. Сол себептен қ оспадағ ы заттың концентрациясын білуіміз ө те қ ажет.
Молекулалық физикада концентрацияның бірнеше тү рлері қ олданылады.
Осы айтылғ андардан (11) жә не (12) ө рнегімен анық талғ ан массалық жә не сандық тығ ыздық тар кө лемдік концентрация қ атарына жатады. Мұ ндай концентрациялардың ө лшем бірліктері болады. Мысалы, 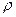 массалық тығ ыздық тың бірлігі
массалық тығ ыздық тың бірлігі  , ал
, ал 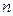 – сандық тығ ыздық тың –
– сандық тығ ыздық тың – 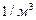 болады.
болады.
Кө птеген физикалық мә селелерді қ арастырғ анда ө лшемсіз концентрацияны қ олдану ың ғ айлы.
Қ оспадағ ы 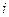 - компоненттің мольдік ү лесі немесе салыстырмалы мольдік концентрациясы
- компоненттің мольдік ү лесі немесе салыстырмалы мольдік концентрациясы 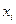 деп, осы компоненттің
деп, осы компоненттің 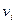 мольдер санының барлық қ оспаның компоненттерінің мольдер санына
мольдер санының барлық қ оспаның компоненттерінің мольдер санына
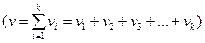 қ атысы арқ ылы анық талатын шаманы айтады, демек
қ атысы арқ ылы анық талатын шаманы айтады, демек
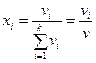
немесе
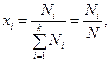 (16)
(16)
мұ ндағ ы 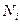 –
– 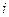 компоненттің бө лшектер саны,
компоненттің бө лшектер саны, 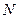 – жалпы молекулалар саны,
– жалпы молекулалар саны, 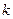 - компоненттер саны.
- компоненттер саны.
Идеал газдар қ оспасы ү шін мольдік ү лесі компоненттердің парциал қ ысымдары 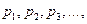 жә не қ оспаның жалпы қ ысымы
жә не қ оспаның жалпы қ ысымы 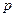 арқ ылы анық талуы мү мкін:
арқ ылы анық талуы мү мкін:
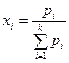 (17)
(17)
Қ оспағ а кіретін заттың қ айсыбір компонентінің дә л сол қ оспадағ ыдай мө лшерде ыдыста жалғ ыз ө зі калғ ан кездегі рі қ ысымы, газ қ оспасының сол компонентінің парциал қ ысымы деп аталады. Онда, газ қ оспасының жалпы р қ ысымы қ оспаның компоненттерінің парциал қ ысымдарының қ осындысына тең болады:
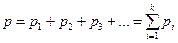 (18)
(18)
Сө йтіп, идеал газ қ оспасының жалпы қ ысымы (18)-ші формуламен анық талады, оны Дальтон заң ы дейді.
Идеал газдың қ оспалары да кә дімгі идеал газ болып келеді.
Осы айтылғ аннан, идеал газ қ оспасының кез келген компонентінің парциал қ ысымы, оның қ оспадағ ы мольдік ү лесінің қ оспаның жалпы қ ысымының кө бейтіндісіне тең болады:
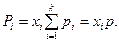 (19)
(19)
Салыстырмалы мольдік концентрациясы бірлік кө лемдегі 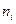 молекулалар саны арқ ылы есептеуге болады:
молекулалар саны арқ ылы есептеуге болады:
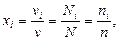 (20)
(20)
мұ ндағ ы 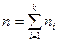 .
.
Кең тарағ ан 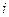 – компоненттің массалық ү лесі немесе салыстырмалы массалық концентрациясы былай анық талады:
– компоненттің массалық ү лесі немесе салыстырмалы массалық концентрациясы былай анық талады:
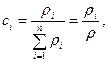 (21)
(21)
мұ ндағ ы 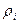 –
– 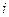 компоненттің тығ ыздығ ы,
компоненттің тығ ыздығ ы, 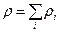 – қ оспаның тығ ыздығ ы.
– қ оспаның тығ ыздығ ы.
Қ оспаның салыстырмалы концентрациясының қ осындысы бірге тең болады, демек
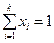 немесе
немесе 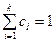 (22)
(22)
Қ оспалардың қ асиеттерін қ арастырғ анда ә р тү рлі араласу ережелерін қ олданады.
Мысалы, қ оспаның қ ұ рамында екі компонент бар делік, онда 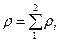 қ оспаның тығ ыздығ ын таза компоненттердің
қ оспаның тығ ыздығ ын таза компоненттердің 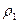 жә не
жә не 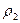 тығ ыздық тары арқ ылы былай анық тауғ а болады:
тығ ыздық тары арқ ылы былай анық тауғ а болады:
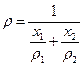 . (23)
. (23)
Қ оспадағ ы 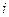 компоненттің мольдік кө лемдік концентрациясы мына тү рде анық талады:
компоненттің мольдік кө лемдік концентрациясы мына тү рде анық талады:
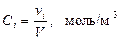 (24)
(24)
мұ ндағ ы, 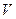 – газдың кө лемі,
– газдың кө лемі, 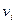 –
– 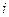 компоненттің мольдер саны.
компоненттің мольдер саны.
Идеал газдың қ оспалары ү шін заттың кө лемдік жә не салыстырмалы мольдік концентрациялары дә л келеді.
Молекула-кинетикалық теорияның негізгі тең деуін шығ ару ү шін алдымен мынадай мә ліметтер қ олданылады:
– бір атомды идеал газ қ арастырылады;
– газ молекулалары ретсіз қ озғ алады. Оның қ озғ алысының барлық бағ ыты бірдей деп алынады;
– газ молекулаларының ө зара соқ тығ ысу саны, олардың ыдыс қ абырғ асымен соқ тығ ысу санына қ арағ анда ө те ескерусіз аз;
– молекулалардың ыдыс қ абырғ асына соқ тығ ысуы абсолютті серпімді;
– молекулалардың ретсіз қ озғ алысын есептеу ү шін қ озғ алыс бағ ыттары ө зара перпендикуляр координата осьтерінің бойында ілгерлемелі қ озғ алысқ а тү седі деп жориды. Уақ ыттың кез-келген мезетінде бір бағ ытта барлық молекулалардың 1/3 оның ішінде 1/6 молекулалар тура бағ ытта, ал 1/6 молекулалар кері бағ ытта қ озғ алады деп есептеледі.
– барлық молекулалардың жылдамдығ ы бірдей 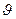 тең деп алынады.
тең деп алынады.
Ойша газ қ ұ йылғ ан ыдыс ішінен табан ауданы 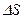 , жасаушысы
, жасаушысы 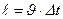 тең болатын тік цилиндрді бө ліп алайық.
тең болатын тік цилиндрді бө ліп алайық.
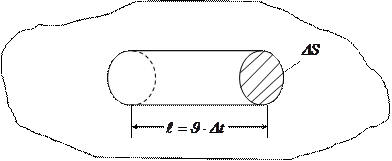
2 - сурет
Сонда, бір бағ ытта қ озғ алатын молекулалардың саны
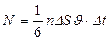
мұ ндағ ы 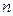 - молекула концентрациясы.
- молекула концентрациясы.
Сонда N молекулалардың ыдыс қ абырғ асына соқ тығ ысқ ан кездегі оғ ан беретін импульсі
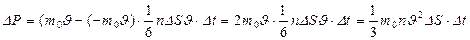 (25)
(25)
мұ ндағ ы 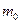 - молекула массасы.
- молекула массасы.
Газ молекулаларының ыдыс қ абырғ асына тү сіретін қ ысымы
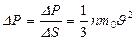 (26)
(26)
Егер идеал газдың 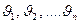 жылдамдық пен қ озғ алатын иолекула болса, онда олардың орташа квадраттық жылдамдығ ы
жылдамдық пен қ озғ алатын иолекула болса, онда олардың орташа квадраттық жылдамдығ ы
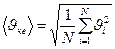
Сонда идеал газдың МКТ негізгі тең деуін жазайық
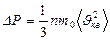 (27)
(27)
оны ә рі қ арай тү рлендірсек, онда
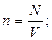
қ ысым
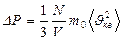
немесе
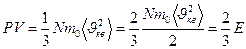 (28)
(28)
жә не
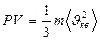 (29)
(29)
немесе
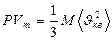 (30)
(30)
Бұ л (27), (28), (29), (30) тең деулерді МКТ негізгі тең деулері деп атайды.
Температура. Температура тү сініктемесі. Жылулық тепе-тең дік.
Молекула-кинетикалық теорияның негізгі тендеуі бойынша идеал газдың қ ысымы, оның 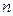 сандық тығ ыздығ ына жә не молекулалардың ілгерілемелі қ озғ алысының орташа кинетикалық энергиясына пропорционал болады.
сандық тығ ыздығ ына жә не молекулалардың ілгерілемелі қ озғ алысының орташа кинетикалық энергиясына пропорционал болады. 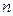 тұ рақ ты болғ анда, газ массасының кө лемі ө згермеген кезде.
тұ рақ ты болғ анда, газ массасының кө лемі ө згермеген кезде.
Тә жірибеден белгілі, тұ рақ ты кө лемдегі газдың қ ысымын бір ғ ана тә сілмен ө згертуге болады: немесе қ ыздырып, немесе суытып. Газды қ ыздырғ анда оның қ ысымы ө седі, ал суытқ анда тө мендейді. Бұ л айтылғ андарды тікелей тә жірибеде бақ ылауғ а болады. Кез келген заттың ыстық немесе суық болуын сипаттайтын ерекше шаманы температура деп атайды. Онда температура заттың жылулық қ асиетін сипаттайтын шама болатындығ ы анық.
Осы айтылғ андардан температура заттың қ ұ рамындағ ы жеке молекулалардың орташа кинетикалық энергиясымен байланысты болуын сеземіз. Физикалық шаша ретінде температураның ерекшелігін қ арапайым тә жірибеден байқ ауғ а болады. Жылылығ ы ә р тү рлі бірнеше денелерді қ атарлап қ оюғ а болады. Мысалы, бізге судың буы судың (сұ йық) ө зінен ыстығ ырақ, ал мұ здан жылы кө рінеді. Бір жағ ынан, осы заттар бір-бірімен тү йісетін болса, онда олардың температуралары тең еле бастайды, демек жылылығ ы бірдей болып, жылулық тепе-тең дік кү йге келеді. Термодинамиканың нө лдік заң ы осы қ асиетпен негізделеді. Егер бір-біріне тә уелсіз екі А жә не В денелер жеке-жеке ү шінші С денемен жылулық тепе-тең дікте болса, онда олар бір-бірімен дә л осындай жылулық тепе-тең дікте болады. Басқ аша айтқ анда жылулық тепе-тең дік жү йенің барлық нү ктелерінде температурасы тең болатынын анық тайды. Бұ л заң термодинамиканың нө лдік заң ы деп аталады.
Физикалық шама ретінде температураны басқ а параметрлермен салыстырғ анда, оның ө згешелігі бар. Ол ө згешелік температураның аддитивтік шама еместігі. Кезкелген денені ойша бірнеше бө лікке бө лейік, онда тұ тас дененің температурасы, оның бө ліктерінің температураларының қ осындысына тең болмайды. Мысалы, дененің кө лемінің барлық бө ліктерін қ осып есептеуге болады, демек кө лем аддитивтік шама.
Температураны ө лшеу тә сілдері кө не заманнан белгілі. Бұ л тә сілдер заттың температурасыш ө згергенде оның қ асиеттері ө згеретінін пайдаланады.
Онда заттың шн қ асиеттерін сипаттайтын шамалар да температура ө згергенде ө згереді. Заттың температурасын ө згерту, оның барлық физикалық қ асиеттеріне ә сер етеді: сызық тық ө лшемдері, олардың серпімділік қ асиеттері, ө ткізгіштердің электрлік кедергілері жә не т.б. ө згереді. Осы ө згерістердің кезкелгенін температураны ө лшеу ү шін қ олдануғ а болады.
Сондық тан, температураны ө лшейтін аспапты, яғ ни термометрді жасау ү шін, қ асиеті температурағ а байланысты ү здіксіз жә не бірсарынды ө згеретін қ андай да бір затты таң дайды, оны термометрлік зат деп айтады. Оғ ан қ оса заттың қ асиетін сииаттайтын белгілі бір шаманы, демек термометрлік шаманы, таң дап алуымыз қ ажет. Мысалы, термометрлік зат – сынап, онда термометрлік шама ретінде оның кө лемін алуғ а болады. Сынаптың кө лемінің ө згерісі температурағ а тура пропорционал, демек сызық тық тү рде ө згереді деп есептеледі. Сұ йық тың кө лемінің температурағ ақ атысты ө згеруі кө птеген термометрлерде қ олданады.
Термометрлік шаманың температурағ а тә уелділігін сандық тү рде сипаттау ү шін, температураның ө лшем бірлігін енгізуіміз керек. Температураның ө лшем бірлігі ретінде " градус" (латынның gradus - адым) тағ айындалғ ан. Ол былай анық талады. Еркін тү рде алынғ ан екі температура аралығ ын алып, оны градус деп аталатын бірдей бө ліктерге бө леміз де, температураның біреуіне белгілі бір сандық мә н тағ айындаймыз. Осы арқ ылы екінші температураның жә не аралық тағ ы кез келген температуралардың мә нін анық тауғ а болады. Сө йтіп, температуралық шкала қ ұ рылады.
Мысалы, ә йгілі Цельсийдің температуралық шкаласында айтылғ ан екі температура (реперлік нү ктелер) ретінде – мұ здың еру температурасы 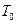 мен судың атмосфералық қ ысымда қ айнау температурасы
мен судың атмосфералық қ ысымда қ айнау температурасы 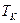 алынғ ан. Осы температуралық интервал бірдей 100 бө лікке бө лінген. Сондық тан, бұ л шкаланың градусы былай анық талады:
алынғ ан. Осы температуралық интервал бірдей 100 бө лікке бө лінген. Сондық тан, бұ л шкаланың градусы былай анық талады: 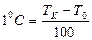 . Осындай тә сілді қ олданып кө птеген термометрлер мен температуралық шкала қ ұ руғ а болады.
. Осындай тә сілді қ олданып кө птеген термометрлер мен температуралық шкала қ ұ руғ а болады.
Ғ ылымның тарихында, мысалы, Реомюр температурылық шкаласы (Париж, 1750 ж.), Цельсий шкаласы (Швеция, 1742 ж.), Фаренгейт пікаласы (Англия, 1724 ж.) орын тапқ ан. Мысалы, Фаренгейт шкаласы қ азіргі заманда АҚ ІІІ-та қ олданады, 1°Ғ =5/9 °С.
Қ азіргі термометрия идеал газдың шкаласы бойынша негізделген. Бұ л термометрлік шкаласы газ термометрі кө мегімен тағ айындалады. Газ термометрі деген идеал газбен толтырылғ ан, қ ысымын ө лшейтін манометрмен жабдық талғ ан жабық ыдыс. Бұ л термометрдің термометрлік заты – идеал газ, ал термометрлік шамасы ретінде тұ рақ ты кө лем кезіндегі газдың қ ысымы алынады. Кө лемі тұ рақ ты болғ анда газдың белгілі массасының қ ысымының температурағ а тә уелділігі сызық тық деп есептеледі. Газ термометрінде термометрлік зат ретінде тө менгі температурада сутегі немесе гелийді, ал жоғ арғ ы температурада азотты пайдаланады.
Бұ л жорамал бойынша судың қ айнау жә не мұ здың еру температураларына сә йкес қ ысымдарының қ атысы, осы температуралардың ө здерінің катысына тең болады:
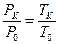 , (31)
, (31)
мұ ндағ ы 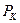 – газ термометріндегі идеал газдың судың
– газ термометріндегі идеал газдың судың 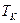 қ айнау температурасындағ ы қ ысымы;
қ айнау температурасындағ ы қ ысымы; 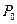 - газ термометріндегі идеал газдың мұ здың еруінің
- газ термометріндегі идеал газдың мұ здың еруінің 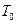 температурасындағ ы қ ысымы.
температурасындағ ы қ ысымы.



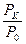 – қ атынасы тә жірибеден анық талады. Кө птеген ө лшеу нә тижелерінен мынандай қ атынас табылды:
– қ атынасы тә жірибеден анық талады. Кө птеген ө лшеу нә тижелерінен мынандай қ атынас табылды: 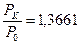 . Онда температуралар қ атынасы да сондай шамағ а тең болады:
. Онда температуралар қ атынасы да сондай шамағ а тең болады:  .
.
Градустың ө лшемін 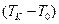 айырмасын жү з бө лікке бө ліп табады:
айырмасын жү з бө лікке бө ліп табады:
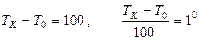 . (32)
. (32)
(31) жә не (32) ө рнектерден мұ здың атмосфералық қ ысымда еритін температурасы 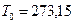 градус, ал судың қ айнау температурасы 373, 15 градус шығ ады.
градус, ал судың қ айнау температурасы 373, 15 градус шығ ады.
Газ термометрімен дененің температурасын ө лшеу ү шін, денені термометрмен тү йістіреді немесе жалғ астырады, содан соң жү йеде жылулық тепе-тең дік орналасқ аннан кейін, термометрдегі газдың қ ысымын ө лшейді. Сө йтіп, дененің температурасы тө мендегі ө рнектен табылады:
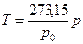 , (33)
, (33)
мұ ндағ ы 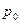 - еріп тұ рғ ан мұ здағ ы термометрдегі газдың қ ысымы.
- еріп тұ рғ ан мұ здағ ы термометрдегі газдың қ ысымы.
Практикада газ термометрі басқ а барлық термометрлерді градуирлеу ү шін қ олданылады.
Идеал газдың температуралық шкаласы бойынша, температураның нольдік мә ні газдың қ ысымы нольге тең болуына сә йкес келеді. Егер термометрлік шкаланың, ноль мә нінде термометрлік шама ноль болса, мұ ндай шкаланы абсолюттік шкала деп атайды. Осы абсолюттік шкала бойынша анық талғ ан температура абсолюттік температура деп аталады жә не Т деп белгіленеді.
Сондық тан газтермометрінің шкаласы абсолюттік болады. Осы шкаланы Кельвин шкаласы деп те атайды. Кельвин шкаласындағ ы температураның ө лшем бірлігін Кельвин градусы немесе кельвин дейді жә не К деп белгілейді.
Кең таралғ ан Цельсий шкаласының градусы Кельвин шкаласының градусымен сә йкестендірілген.
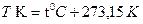
деп жазуымызғ а болады. Мұ ндағ ы, 273, 15 саны Цельсий шкаласындағ ы температураның нө лдік мә ні, мұ здың атмосфералық қ ысымда еритін температурасына сә йкес. Цельсий шкаласындағ ы температура белгісі  болады.
болады.
Барометрлік формула
Молекулалық -кинетикалық теорияның негізгі тең деулерін жазғ ан кезде молекулаларғ а сырттан ешқ андай кү ш ә сер етпейді. Сондық тан молекулалар ыдыс ішінде жылдамдық тары бойынша біртекті таралады деп жорығ анбыз.
Бірақ кез-келген молекула жердің тартылу ө рісінде орналасқ андық тан оғ ан ауырлық кү ші ә сер етеді. Молекула ә рдайым жылулық, хаосты қ озғ алыста болғ андық тан, олар тартылу ө рісінде белгілі биіктікке байланысты ө згеріп отырады.
Атмосфералық 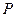 қ ысымның
қ ысымның 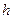 биіктікке тә уелділік ө рнегін барометрлік формула деп атайды.
биіктікке тә уелділік ө рнегін барометрлік формула деп атайды.
Барометрлік формуланы шығ ару ү шін мынадай алғ ы шарттар жү зеге асырылады:
– тартылу ө рісі біртекті;
– температура тұ рақ ты;
– барлық молекулалардың массалары бірдей;
– еркін тү су ү деуі тұ рақ ты.
Егер атмосфералық қ ысым 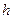 биіктікте
биіктікте 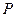 болса, онда
болса, онда 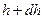 биіктікте ол
биіктікте ол 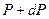 (
(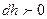 ,
, 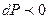 биіктік ө скен сайын қ ысым тө мендейді).
биіктік ө скен сайын қ ысым тө мендейді).

3 - сурет
Сонда 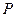 мен
мен 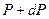 айырымы тік цилиндрдің бірлік табан ауданы мен
айырымы тік цилиндрдің бірлік табан ауданы мен 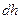 биіктігіне сә йкес кө леміндегі газ салмағ ына тең.
биіктігіне сә йкес кө леміндегі газ салмағ ына тең.
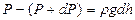
мұ ндағ ы 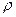 газдың
газдың 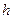 биіктіктегі тығ ыздығ ы.
биіктіктегі тығ ыздығ ы.
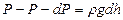
немесе
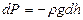 (34)
(34)
Енді Менделеев-Клайперон тең деуінен газ тығ ыздығ ы 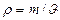
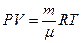 немесе
немесе 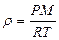 (35)
(35)
мұ ндағ ы 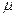 - молярлық масса, сонда (34), (35)-ші тең деулерден
- молярлық масса, сонда (34), (35)-ші тең деулерден
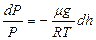 (36)
(36)
Газ дең гейі 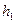 -ден
-ден 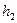 -ге кө терілген қ ысым
-ге кө терілген қ ысым 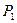 -ден
-ден 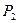 -ге ө згереді.
-ге ө згереді.
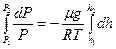
Бұ дан
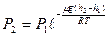 (37)
(37)
Егер бастапқ ы биіктік 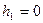 ,
, 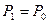 ,
, 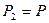 , ал
, ал  , деп алсақ, онда (37) тең деуді былай жазамыз:
, деп алсақ, онда (37) тең деуді былай жазамыз:
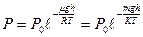
немесе молекулалық -кинетикалық теорияның негізгі тең деуін 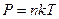 еске алсақ, онда
еске алсақ, онда
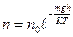 (38)
(38)
мұ ндағ ы 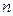 мен
мен 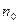 биіктіктердің аралығ ы
биіктіктердің аралығ ы 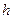 болатын нү ктелердегі бірлік кө лемге келетін молекулалар саны.
болатын нү ктелердегі бірлік кө лемге келетін молекулалар саны.
Негізгі ә дебиеттер:
1. Ә лжанов К.К., Қ ұ саинов К.К., Мү сенов К.Қ., Дә рібеков С. Молекулалық физика. Қ арағ анды. Қ арМУ.2003
2. Қ ұ лбекұ лы М. Молекулалық физика жә не термодинамика. Алматы, Қ арасай баспасы. 2005
3. Қ ойшыбаев Н. Молекулалық физика. Алматы, Зият пресс баспасы. 2005
Қ осымша ә дебиеттер:
1. Қ ойшыбаев Н., Шарық баев А.О. Физика. Алматы. 2001
2. Савельев И.В. Жалпы физика курсы. М., Наука, 1986.
3. Дә рібеков С. Материалдар физикасының негіздері. Қ арМУ 2005.