Теоретичні відомості. Дослідження невизначеності цілей і ситуацій

Лабораторна робота № 1

Дослідження невизначеності цілей і ситуацій

Мета лабораторної роботи - вирішення формалізованих завдань розкриття неопределенностейцілей і ситуацій в системному аналізі складних систем управління.

Порядок виконання роботи

1. Вивчити теоретичний матеріал по розкриттю неопределенностейцілей і ситуацій.

2.Познайомитися з прикладами виконання рішення задачі розкриття невизначеності цілей і ситуацій.

3.Для конкретного варіанту вирішити задачу розкриття неопределенностей

цілей і ситуацій.

4.Оформити звіт по лабораторній роботі.

Теоретичні відомості

Невизначеність є типовою властивістю практичних завдань системного аналізу (СА), що обумовлене різноманіттям цілей, властивостей і особливостей об'єктів СА.

У загальному випадку при розгляді цілісного об'єкту з погляду формулювання функції мети завдання можна розглядати в загальному вигляді

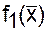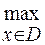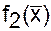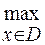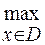® , ® ,... ® (1)

Оскільки функції, k=1, 2..., n є різними (за типом), то екстремум кожної функції досягається при своєму значенні і не можна знайти таке значення, при якому умови (1) виконуються одночасно для всіх функцій. Тому виникає завдання знаходження такого значення 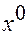, при якому буде забезпечений раціональний компроміс заданих цілей.

Для знаходження раціонального компромісу розроблено два основні підходи:

1) Суть першого підходу - виключити з аналізу свідомо неприйнятні варіанти;

2) Суть другого - знайти способи приведення багатоцільового завдання до звичайного завдання з одним критерієм.

У основі першого підходу лежить ідея, запропонована Парето: спробувати скоротити множину початкових варіантів шляхом виключення з неформального аналізу таких варіантів, які свідомо є непридатними. Реалізація цієї ідеї здійснюється таким чином.

Покладемо, що зроблений деякий вибір вектора - позначимо його значення 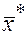. Робимо тепер деякий інший вибір такий, що для всіх цільових функцій

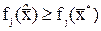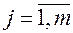, (2)

причому, хоч би одне з нерівність строга. Очевидно, що вибір 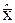переважно 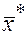.Тому всі вектори із значенням 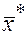, для яких виконується (2), слід виключити з даного аналізу. Піддавати неформальному аналізу, зіставляти між собою слід ті вектори 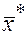, для яких не існує такого значення 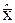, хоч би для однієї із заданих цільових функцій, для якого виконується нерівність (2).

Множина всіх значень 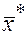, для яких неможливо підібрати з умови (2), називається множиною Парето, а вектор 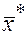називається не покращуваним вектором результатів (вектор Парето).