Множина Парето

Відома множина цільових функцій , заданих на множині , де

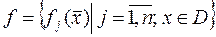
Знайдемо таку множину Г значень 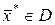, яка ділить початкову множину на дві множини: множина П і множина , де

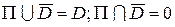(3)

Множина П складається з таких значень , для яких для всіх виконується умова

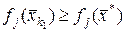(4)

Множина П визначається співвідношенням

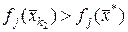Множина складається з таких , для яких хоч би для однієї функції виконується умова . Множина описується таким чином

Вектор 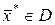прийнято називати вектором непокращуваних для множини результатів, а множину , що задовольняє умові (4), називають множиною Парето.

Через умову (4) множина 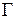є межею множини Парето. У

відповідності з (3) маємо .

Тому всі варіанти, які належать 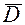, виключаються з розгляду.

Приклад. Хай потрібно виділити множина Парето в області

Розіб'ємо задану множину 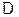на три множини: .

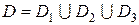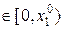
де, 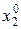точка значення , при якому 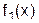досягає максимуму

,

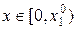
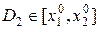, де 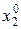таке значення , при якому 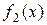досягає максимуму

, .

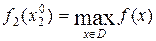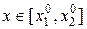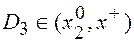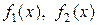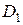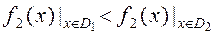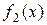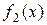. Порівнюючи значення функцій у областях та , маємо тобто значення функції для будь-якого менше, ніж значення для будь-якого . Для маємо 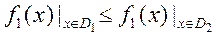(соїзмеріми), тобто область 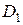свідомо гірше за область по цільовій функції .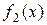

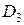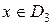Аналогічно, для області значення функції для будь-якого менше, ніж значення для будь-якого , тобто 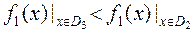. А для 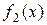маємо (соїзмеріми), тобто область 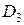свідомо гірше за область по цільовій функції . Таким чином, з області виключається область 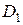і область 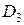. Область є множиною Парето. Для даної області виконуються критерії:

.

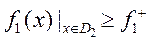
Відповідно до принципу Парето раціональне рішення модельної задачі (раціональний компроміс в багатоцільовому завданні) необхідно шукати серед , що належать множині Парето. Принцип Парето не виділяє єдиного рішення, але він дозволяє звузити множина можливих альтернативних рішень. У даному прикладі раціональне рішення необхідно шукати в області . Але питання про те, яке рішення (або яке значення ) є оптимальним - залишається відкритим.

У всіх даних випадках множина Парето дозволяє отримати додаткову інформацію, яка дає якісну оцінку при зіставленні різних варіантів. На розглянутому прикладі видно, що в крапці 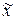має місце рівність

= .

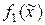Який з розглянутих варіантів є переважним визначає ЛПР. Якщо ЛПР вважає, що критерії рівносильні, то раціональним є варіант 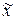, коли 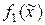= . Якщо важливішою є мета , то, очевидно, раціональне рішення лежить в інтервалі . Якщо важливішою є мета 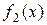, то раціональне рішення лежить в інтервалі 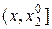. Проте, в двох останніх випадках конкретний ступінь переваги єдиній меті над іншою залишається суб'єктивною мірою ЛПР.