Определение последовательности, способы задания, операции над последовательностями. Предел последовательности.

Лекция №5

ПОСЛЕДОВАТЕЛЬНОСТИ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ

Определение последовательности, способы задания, операции над последовательностями. Предел последовательности.

Определение 1. Последовательностью действительных чисел называется отображение , определенное на множестве всех натуральных чисел Кратко ее обозначают символом 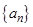. Число 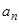называется общим членом последовательности. Иными словами, последовательность считается заданной, если указан способ получения любого ее элемента.

Пример 1. . Тогда имеем , 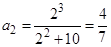и т.д.

Заметим, что обратная операция – нахождение выражения 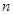-го члена последовательности по нескольким первым членам этой последовательности – не имеет однозначного решения.

Последовательности могут быть заданы и соотношением, задающим выражение 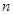-го члена последовательности через ее предыдущие члены.

Пример 2. Равенства 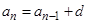; 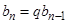, , 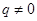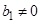(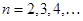) определяют соответственно арифметическую и геометрическую прогрессии. Рекуррентно задана и последовательность Фибоначчи 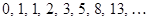, в которой каждый член (начиная с третьего) равен сумме двух предыдущих. Полное рекуррентное задание этой последовательности таково: , , , .

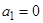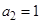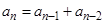Определение 2. Последовательност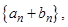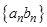и и 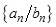называются соответственно суммой, разностью, произведением и частным двух последовательносте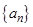й и 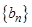(для частного ).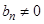