
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Предел последовательности.
|
|
Рассмотрим последовательность с общим членом 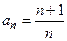 , при
, при 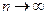 члены последовательности неограниченно приближаются к 1. На языке математического анализа выражение «неограниченно приближается» означает, что какое бы малое число
члены последовательности неограниченно приближаются к 1. На языке математического анализа выражение «неограниченно приближается» означает, что какое бы малое число  мы ни взяли, начиная с некоторого номера
мы ни взяли, начиная с некоторого номера  все члены последовательности будут сколь угодно мало отличаться от
все члены последовательности будут сколь угодно мало отличаться от 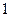 .
.
Определение 1. Число 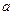 называется пределом последовательности
называется пределом последовательности  , если для любого положительного числа
, если для любого положительного числа  существует такой номер
существует такой номер  , что при всех
, что при всех 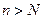 выполняется неравенство
выполняется неравенство  . Обозначение
. Обозначение 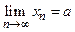 . Кратко определение предела записывается так:
. Кратко определение предела записывается так: 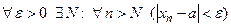 .
.
Неравенство  равносильно двойному неравенству
равносильно двойному неравенству 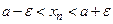 , которое показывает, что элементы
, которое показывает, что элементы 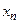 при
при 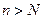 находятся в окрестности точки
находятся в окрестности точки 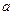 . Поэтому геометрически определение предела формулируется так.
. Поэтому геометрически определение предела формулируется так.
Определение 2. Число 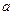 называется пределом последовательности
называется пределом последовательности  , если для любой
, если для любой  -окрестности точки
-окрестности точки 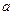 найдется такое натуральное число
найдется такое натуральное число 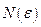 , что все значения
, что все значения 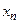 , для которых
, для которых 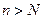 , попадут в
, попадут в  -окрестность точки
-окрестность точки 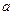 .
.
Ясно, что чем меньше  тем больше число
тем больше число  , но в любом случае внутри
, но в любом случае внутри  -окрестности точки
-окрестности точки 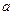 находится бесконечное число членов последовательности, а вне ее находится лишь конечное число членов последовательности.
находится бесконечное число членов последовательности, а вне ее находится лишь конечное число членов последовательности.
Выясним геометрический смысл определения предела последовательности.
Неравенство | xn – a|< ε равносильно неравенствам -ε < xn - а < ε или а - ε < xn < a+ ε, которые показывают, что элемент xn находится в ε -окрестности точки а.

Рис.1
Поэтому определение предела последовательности геометрически
можно сформулировать так: число а называется пределом последовательности {xn}, если для любой ε -окрестности точки а найдется натуральное число N, что все значения xn, для которых n > N, попадут в ε -окрестность точки а (см. рис. 1).
Последовательность, имеющая предел называется сходящейся, а последовательность, не имеющая предела, называется расходящейся.
Например, последовательность 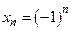 не имеет предела.
не имеет предела.
Теорема 1. Сходящаяся последовательность имеет только один предел.
Для доказательства утверждения применим метод от противного.
Пусть 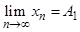 и
и 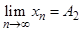 . Если А 1≠ А 2, то фиксируем непересекающиеся окрестности U (A 1), U (A 2) точек А 1, А 2. В качестве таковых можно взять, например, δ -окрестности этих точек при δ <
. Если А 1≠ А 2, то фиксируем непересекающиеся окрестности U (A 1), U (A 2) точек А 1, А 2. В качестве таковых можно взять, например, δ -окрестности этих точек при δ <  │ А 1– А 2│. По определению предела найдем числа N 1, N 2 такие, что все члены последовательности
│ А 1– А 2│. По определению предела найдем числа N 1, N 2 такие, что все члены последовательности 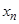 с номерами n > N 1 попадут в окрестность точки А 1, а с номерами n > N 2 в окрестность точки А 2. Тогда при n > max{ N 1, N 2} получим xn
с номерами n > N 1 попадут в окрестность точки А 1, а с номерами n > N 2 в окрестность точки А 2. Тогда при n > max{ N 1, N 2} получим xn  U (A 1)
U (A 1) 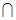 U (A 2). Но это невозможно, так как пересечение U (A 1)
U (A 2). Но это невозможно, так как пересечение U (A 1) 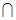 U (A 2)=
U (A 2)= 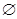 .
.
Теорема 2. Если числовая последовательность имеет конечный предел, то она ограничена.
Доказательство: Пусть  . Полагая в определении предела ε =1, найдем номер N такой, что
. Полагая в определении предела ε =1, найдем номер N такой, что  n > N справедливо неравенство │ xn – A │ < 1. Значит, при n > N имеем
n > N справедливо неравенство │ xn – A │ < 1. Значит, при n > N имеем
│ xn │ < │ A │ +1. Если же теперь взять М > max{│ x 1│, │ x 2│, …, │ xn │, │ A │ +1},
то получим, что  n > N все члены последовательности ограничены │ xn │ < М.
n > N все члены последовательности ограничены │ xn │ < М.
Пример 1. Используя определение предела последовательности, докажем, что 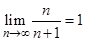 .
.
Решение. Зададим произвольное  и рассмотрим модуль разности между
и рассмотрим модуль разности между 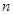 -м членом последовательности и числом 1:
-м членом последовательности и числом 1:  . В соответствии с определением предела последовательности мы должны указать номер
. В соответствии с определением предела последовательности мы должны указать номер  такой, что
такой, что 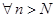 выполняется неравенство
выполняется неравенство
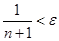 . (1)
. (1)
Для отыскания номера  решим неравенство (1) относительно
решим неравенство (1) относительно 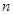 . Получим
. Получим
 . (2)
. (2)
Из неравенства (2) следует, что в качестве  можно взять целую часть числа
можно взять целую часть числа 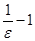 :
:  . В самом деле, если
. В самом деле, если 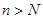 , то
, то  , т.е. справедливо неравенство (2), а значит,
, т.е. справедливо неравенство (2), а значит, 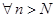 выполняется неравенство (1).
выполняется неравенство (1).
Итак, для произвольного  мы указали такой номер
мы указали такой номер  , что
, что  выполняется неравенство
выполняется неравенство 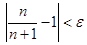 . Это и означает по определению предела последовательности, что
. Это и означает по определению предела последовательности, что 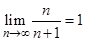 .
.