Метод Гаусса решения СЛАУ

Рассмотрим СЛАУ с произвольным числом уравнений и произвольным числом неизвестных

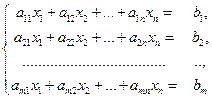(3)

и соответствующую расширенную матрицу 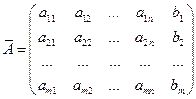. (4)

Между СЛАУ (3) и расширенными матрицами (4) существует взаимно однозначное соответствие. Идея метода Гаусса заключается в том, что над СЛАУ (3) и над соответствующей матрицей (4) одновременно проводятся операции, не меняющие множество решений (3) и упрощающих матрицу и систему таким образом, что решение СЛАУ (3) становится очень простым.

Иногда, говоря о методе Гаусса, рассматривают действия только с системой (3). Мы будем рассматривать только преобразования над строками матрицы (4).

Определение 1. Следующие операции называются элементарными преобразованиями над строками матрицы:

1) перемена местам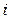и -й и 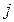-й строк матрицы,

2) умножение 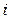-й строки матрицы на число ,

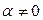3) прибавление к 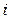-й строке матрицы 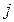-й строки, умноженной на число ,

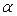4) вычеркивание нулевой троки матрицы.

Теорема 2. Элементарные преобразования над строками расширенной матрицы не меняют множества решений соответствующей СЛАУ.

Доказательство. Относительно операций 1), 2), 4) утверждение является очевидным.

Рассмотрим преобразование № 3. Установим, что оно не уменьшает множество решений соответствующего СЛАУ. В самом деле, если числа 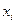, 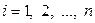являются решением СЛАУ, то при подстановке этих чисел верным является каждое уравнение СЛАУ, в частност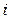и, -е и 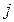-е уравнения. Следовательно, и после умножения 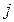-го уравнения на число 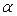оно остается верным. А при сложении двух верных равенств получается верное равенство. Отсюда после проведения преобразования 3) прежнее решение СЛАУ остается решением новой системы. А теперь проведем новое преобразование типа 3): к 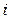-й строке матрицы прибавим 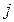-ю строку, умноженной на число 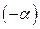. Оно также не уменьшает множество решений СЛАУ, но приводит нас к прежней СЛАУ. Так как при каждом из этих двух преобразований множество решений СЛАУ не уменьшается, а в итоге осталось прежним, то мы делаем вывод, что каждый раз множество решений СЛАУ не изменялось. Теорема доказана.

Пример 2. Решите систему 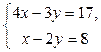методом Гаусса.

Рассмотрим расширенную матрицу СЛАУ 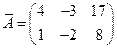и приведем ее к треугольному виду, используя элементарные преобразования над строками матрицы. Поменяем местами 1-ю и 2-ю строки и к полученной 2-й строкбе прибавим 1-ю, умноженную на (-4). Полученная матрица 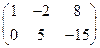соответствует СЛАУ 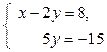может быть легко решена «снизу вверх». Вначале найдем 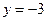, а затем .

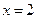Пример 3. Решите систему 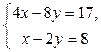методом Гаусса.

Рассмотрим расширенную матрицу СЛАУ 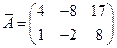и упростим ее, используя элементарные преобразования над строками матрицы. Поменяем местами 1-ю и 2-ю строки и к полученной 2-й строке прибавим 1-ю, умноженную на (-4). Полученная матрица 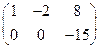соответствует СЛАУ 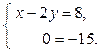Очевидно, эта система не имеет решений.

Пример 4. Решите систему 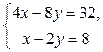методом Гаусса.

Рассмотрим расширенную матрицу СЛАУ 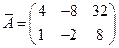и упростим ее, используя элементарные преобразования над строками матрицы. Поменяем местами 1-ю и 2-ю строки и к полученной 2-й строке прибавим
1-ю, умноженную на (-4). Полученная матрица 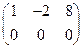преобразуется к виду 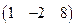и соответствует СЛАУ 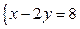, состоящей из одного уравнения. Очевидно, эта система имеет бесконечно много решений. В этом случае мы должны указать в ответе все эти решения. Это можно сделать разными способами.

Ответ 1. 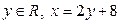. Ответ 2. .

Пример 5. Решите систему 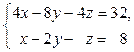методом Гаусса.

Рассмотрим расширенную матрицу СЛАУ и упростим ее, используя элементарные преобразования над строками матрицы. Поменяем местами 1-ю и 2-ю строки и к полученной 2-й строке прибавим 1-ю, умноженную на (-4). Полученная матрица преобразуется к виду 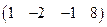и соответствует СЛАУ , состоящей из одного уравнения. Бесконечное число решений запишем двумя способами.

Ответ 1. 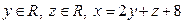. Ответ 2. .

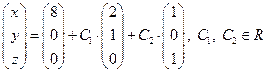Подведем некоторые итоги. СЛАУ может не иметь решений, в этом случае система называется несовместной. СЛАУ будет несовместной тогда и только тогда, когда после приведения к треугольному виду расширенной матрицы СЛАУ последняя строка состоит из нулей и единственного, отличного от 0, последнего элемента в строке.

СЛАУ называется совместной, если она имеет хотя бы одно решение. Совместная система имеет либо единственное решение, либо бесконечное число решений, зависящее от одного или нескольких параметров. В последнем случае число параметров называют размерностью множества решений СЛАУ. Точный смысл слова «размерность» мы изучим чуть позже. Также для точной формулировки этих результатов нам понадобится понятие «ранг матрицы». Мы вернемся к этим вопросам немного позже.