
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Геометрический вектор, линейные операции над векторами
|
|
Определение 1. Геометрическими векторами называются направленные отрезки, которые считаются равными, если длины отрезков и их направления совпадают, и для которых введены операции сложения векторов и умножения вектора на число по следующим правилам:
Пусть заданы 2 вектора 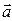 и
и  , тогда суммой этих векторов
, тогда суммой этих векторов  называется вектор
называется вектор 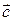 , идущий из начала вектора
, идущий из начала вектора 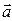 в конец вектора
в конец вектора  , если начало вектора
, если начало вектора  приставлено к концу вектора
приставлено к концу вектора 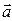 .
.
Пусть задан вектор 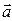 и число
и число 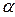 , тогда произведением вектора
, тогда произведением вектора 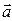 на число
на число 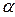 , называется вектор
, называется вектор  , по длине равный длине вектора
, по длине равный длине вектора 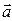 , умноженной на модуль числа
, умноженной на модуль числа 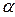 , одинаково направленный с вектором
, одинаково направленный с вектором 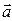 при
при 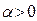 и противоположно направленный с вектором
и противоположно направленный с вектором 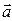 при
при  .
.
Отметим некоторые обозначения и выводы из определения 1.
Пусть у вектора 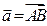 начальной точкой является точка
начальной точкой является точка 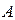 , а конечной точкой – точка
, а конечной точкой – точка 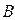 . Тогда
. Тогда  ,
, 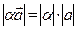 . Вектор, начало и конец которого совпадают, называется нулевым вектором, т. е.
. Вектор, начало и конец которого совпадают, называется нулевым вектором, т. е. 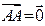 . Обычным образом определяется разность векторов.
. Обычным образом определяется разность векторов.
Введенные операции обладают следующими свойствами: 1)  - коммутативность, 2)
- коммутативность, 2)  - ассоциативность, 3)
- ассоциативность, 3) 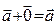 - существование нулевого элемента, 4)
- существование нулевого элемента, 4) 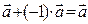 существование противоположного элемента
существование противоположного элемента 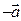 , 5)
, 5) 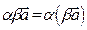 , 6)
, 6) 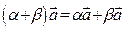 дистрибутивность для числовых коэффициентов, 7)
дистрибутивность для числовых коэффициентов, 7) 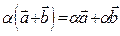 - дистрибутивность для векторов, 8)
- дистрибутивность для векторов, 8) 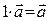 .
.
Познакомимся с понятиями линейной зависимости, линейной независимости векторов, базисом и координатами.