Статистика Дарбина-Уотсона (DW)

Выполнимость предпосылки Гаусса-Маркова о независимости случайных отклонений между собой при разных наблюдениях(cov(ε _i, ε _j) = 0 – отсутствие автокорреляции) проверяют с помощью статистики Дарбина-Уотсона DW.

При этом обычно проверяется некоррелированность не любых случайных отклонений, а только соседних. Соседними обычно считаются соседние во времени (при рассмотрении временных рядов) или по возрастанию объясняющей переменной x (в случае пространственной выборки) значения ε _i. Для этих величин несложно рассчитать коэффициент корреляции, называемый коэффициентом автокорреляции первого порядка:

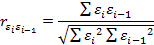
На практике для анализа коррелированности отклонений вместо коэффициента корреляции используют тесно с ним связанную статистику Дарбина-Уотсона DW, рассчитываемую по формуле:

Здесь сделано допущение, что при больших n выполняется соотношение: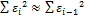

Тогда

Нетрудно заметить, что если 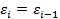, то 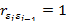(положительная автокорреляция) и W= 0.

Если 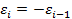, то 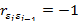(отрицательная автокорреляция) и DW= 4.

Во всех других случаях 0< DW < 4.

При случайном поведении отклонений можно предположить, что в одной половине случаев знаки последовательных отклонений совпадают, а в другой – противоположны. Так как абсолютная величина отклонений в среднем предполагается одинаковой, то можно считать, что в половине случаев 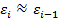, а в другой 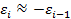. Тогда

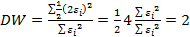и 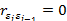(автокорреляция отсутствует).

Таким образом, необходимым условием независимости случайных отклонений является близость к двойке значения статистики Дарбина-Уотсона.

Разработаны специальные таблицы критических точек статистики Дарбина-Уотсона, позволяющие при данном числе наблюдений n, количестве объясняющих переменных m и заданном уровне значимости α определять границы приемлемости (критические точки) наблюдаемой статистики DW.

Для заданных α, n, m в таблице указываются два числа: d_l – нижняя граница и d_u – верхняя граница. Для проверки гипотезы об отсутствии автокорреляции отклонений используется числовой отрезок:

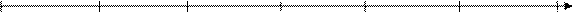0 d_l d_u 2 4- d_u 4- d_l 4

Положительная Отсутствие Отрицательная

автокорреляция автокорреляции автокорреляция

Область неопределенности

Выводы осуществляются о следующей схеме:

· Если DW < d_l, то присутствует положительная автокорреляция отклонений.

· Если DW > 4- d_l, то присутствует отрицательная автокорреляция отклонений.

· Если d_u < DW < 4- d_u, то автокорреляция отклонений отсутствует.

· Если d_l < DW < d_u или 4- d_u < DW < 4- d_l, то гипотеза об отсутствии автокорреляции не может быть ни принята, ни отклонена.

Не обращаясь к таблице критических точек Дарбина-Уотсона, можно пользоваться «грубым» правилом и считать, что автокорреляция остатков отсутствует, если 1, 5< DW < 2, 5.

При наличии автокорреляции отклонений полученное уравнение регрессии обычно считается неудовлетворительным.