Ошибки аппроксимации

Практически всегда фактические значения результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии. Чем меньше это отличие, тем ближе будут теоретические значения подходить к эмпирическим, следовательно, тем лучше подобрано уравнение регрессии. Величина отклонений фактических значений от расчетных результативного признака (у - y_х) по каждому наблюдению представляет собой абсолютную ошибку аппроксимации. Число ошибок соответствует размеру совокупности. В отдельных случаях ошибка аппроксимации может оказаться равной нулю (когда в одном наблюдении фактическое и теоретическое значения результата совпадают). Отклонения (у- y_х) несравнимы между собой за исключением величины, равной нулю.

Для сравнения отклонений относительно фактических значений используются их величины, выраженные в процентах. Поскольку (у - y_х) может быть как положительной, так отрицательной величиной, то ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю

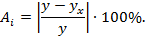
Эти ошибки уже поддаются сравнению, но они оценивают каждое наблюдение в отдельности. Такую ошибку принято называть относительной ошибкой аппроксимации.

Чтобы оценить качество модели в целом, можно определить среднюю ошибку аппроксимации, представляющую собой среднее арифметическое относительных ошибок аппроксимации по всем наблюдениям, включаемым в модель:

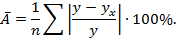
Модель считается подобранной достаточно хорошо, если средняя ошибка аппроксимации не превышает 8-10%.