Закон Био-Савара-Лапласа

Французские ученые Ж. Био и Ф. Савар в 1820 г. провели исследования магнитных полей, создаваемых постоянными токамив проводниках различной формы. Результаты их опытов обобщил П. Лаплас и установил зависимость, которая получила название закона Био-Савара-Лапласа. Согласно этому закону магнитное поле любого тока может быть вычислено как векторная сумма (суперпозиция) полей, создаваемых отдельными элементарными участками тока. Когда ток течет по тонкому проводу, можно ввести понятие элемента тока I× 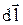, где I – сила тока, dl – элемент длины провода, 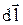- вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с направлением тока. А индукция 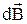элемента тока в вакууме (в воздухе) согласно опытам равна:

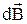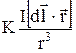= , (22.1)

где 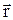- радиус-вектор, проведенный из элемента тока в рассматриваемую точку; а К – коэффициент пропорциональности, зависящий от выбора единиц измерения (в СИ К = m₀/4p, m₀ - магнитная постоянная).

Следовательно, в СИ формула (22.1) имеет вид

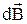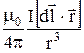= , (22.2)

Из (22.2) следует, что модуль магнитной индукции в точке, удаленной на расстояние r от элемента тока, равен:

dB = 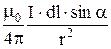, (22.3)

где a - угол между 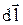и 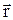(рисунок 29).

Направление вектора 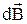перпендикулярно к 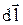и 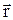, т. е. перпендикулярно к плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление 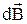, если поступательное движение винта соответствует направлению тока в элементе.

Формула (22.2) носит название закона Био-Савара-Лапласа. Магнитная постоянная m₀ = 4p× 10^-7 единицы СИ. Это значение m₀ непосредственно следует из определения единицы силы тока ампер, которое будет дано в § 5.24. Сама же единица для измерения m₀ в СИ получила название Гн/м (генри на метр, см. § 6.30).

Расчет характеристик магнитного поля (индукции ) по приведенным формулам в общем случае довольно сложен. Однако если распределение тока имеет определенную симметрию, то применение закона Био-Савара-Лапласа совместно с принципом суперпозиции позволяет довольно просто рассчитать конкретные поля.

Применим формулу (22.3) для вычисления магнитного поля прямого тока. Найдем индукцию магнитного поля, создаваемого тонким прямым проводом в точке А (рисунок 30), удаленной на расстояние R от оси провода. Длину провода будем считать весьма большой по сравнению с R. В этом случае направление магнитного поля всех элементов тока провода одинаково (перпендикулярно к плоскости рисунка 30), и поэтому можно складывать модули индукций отдельных элементов тока. Индукция магнитного поля какого-либо элемента проводника dl с током I выражается формулой (22.3). Из рисунка 30 видно, что

, .

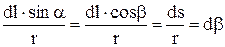Подставляя эти выражения в (22.3), мы находим, индукция магнитного поля, создаваемого элементом провода, равна

dB = = .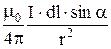

Угол b для всех элементов бесконечного прямого повода изменяется в пределах от -p/2 до +p/2. Поэтому для полной индукции поля получаем

В = = = .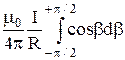

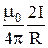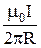Таким образом, магнитная индукция поля прямого тока определяется формулой:

В = 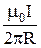. (22.4)

Применяя закон Био-Савара-Лапласа (22.3), найдем индукцию магнитного поля в вакууме в центре кругового тока (рисунок 31). В этом случае все элементы проводника перпендикулярны к радиус-вектору 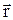и sina = 1. Расстояние всех проводников в центре круга одинаково и равно радиусу круга R. Поэтому (22.3) дает:

.

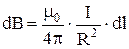Все элементы тока создают магнитное поле одинакового направления, перпендикулярное к плоскости витка, и поэтому полная индукция поля в центре кругового витка равна:

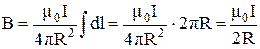. (22.5)

Направление магнитного поля находим по правилу правого винта, который нужно расположить перпендикулярно к плоскости витка; при вращении головки винта по кругу в направлении протекания тока поступательное движение винта укажет ориентацию поля (см. рисунок 31).

Для описания магнитного поля наряду с магнитной индукцией широко используют еще другую величину – напряженность магнитного поля. Если – магнитная индукция в какой-либо точке поля в вакууме (в воздухе), то напряженностью магнитного поля в той же точке поля называется:

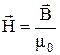. (22.6)

Так как µ₀есть положительная скалярная величина, то направления векторов 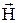и совпадают. Принимая во внимание (22.6), (22.2) и (22.3), можем записать уравнения выражающие закон Био-Савара-Лапласа для напряженности магнитного поля:

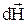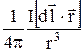= ; dН = . (22.7)

С учетом (22.6) выражения для напряженности магнитного поля прямого тока и кругового тока имеют вид (сравните с индукциями для соответствующих случаев (22.4) и (22.5)):

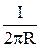Н = и Н = 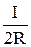. (22.8)

Из (22.8) следует, что напряженность магнитного поля имеет размерность ампер на метр (А/м).