
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Графический метод решения тригонометрических уравнений
|
|
Приведем примеры, применения графического метода решения тригонометрических уравнений и неравенств, который дает возможность определить корни намного проще, чем при аналитическом способе решения.
Пример 6. Решите уравнение: cos t = 2sin t – 1.
Дополним уравнение тождеством sin 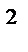 t + cos
t + cos 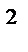 t = 1 и рассмотрим систему двух уравнений:
t = 1 и рассмотрим систему двух уравнений:
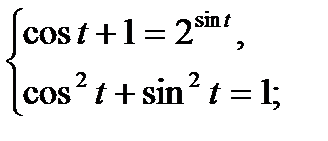
Введём обозначения x = cos t, y = sin t и решим графически систему, состоящую из двух уравнений:



Рис. 8
Графическое решение системы показано на рис. 8. Проведя радиус-векторы точек пересечения единичной окружности с графиком y = log2(x+1), получим:
α 1  48°
48°
α 2 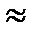 -117°
-117°
t1 = α 1 + 360°n t1 = 48° +360°n
t2 = α 1 + 360°n t2 = -117° + 360°n, где n, k  Z.
Z.
Пример 7. Решите уравнение: 8tg t – 4ctg2 t – 4ctg t + 23 = 0.
Дополним уравнение тождеством ctg t · tg t = 1 и рассмотрим систему двух уравнений:

Введём обозначения x = ctg t, y = tg t и решим графически систему, состоящую из двух уравнений:
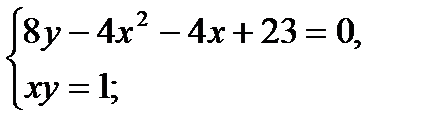

Преобразуем первое уравнение системы:
y = 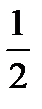 (x2 + x -
(x2 + x -  ) =
) = 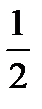 ((x2 +2∙ x∙
((x2 +2∙ x∙ 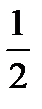 +
+  ) -
) -  -
-  ) =
) = 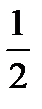 ((x +
((x + 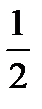 )2 – 6) =
)2 – 6) =
= 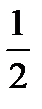 (x +
(x + 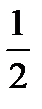 )2 – 3.
)2 – 3.
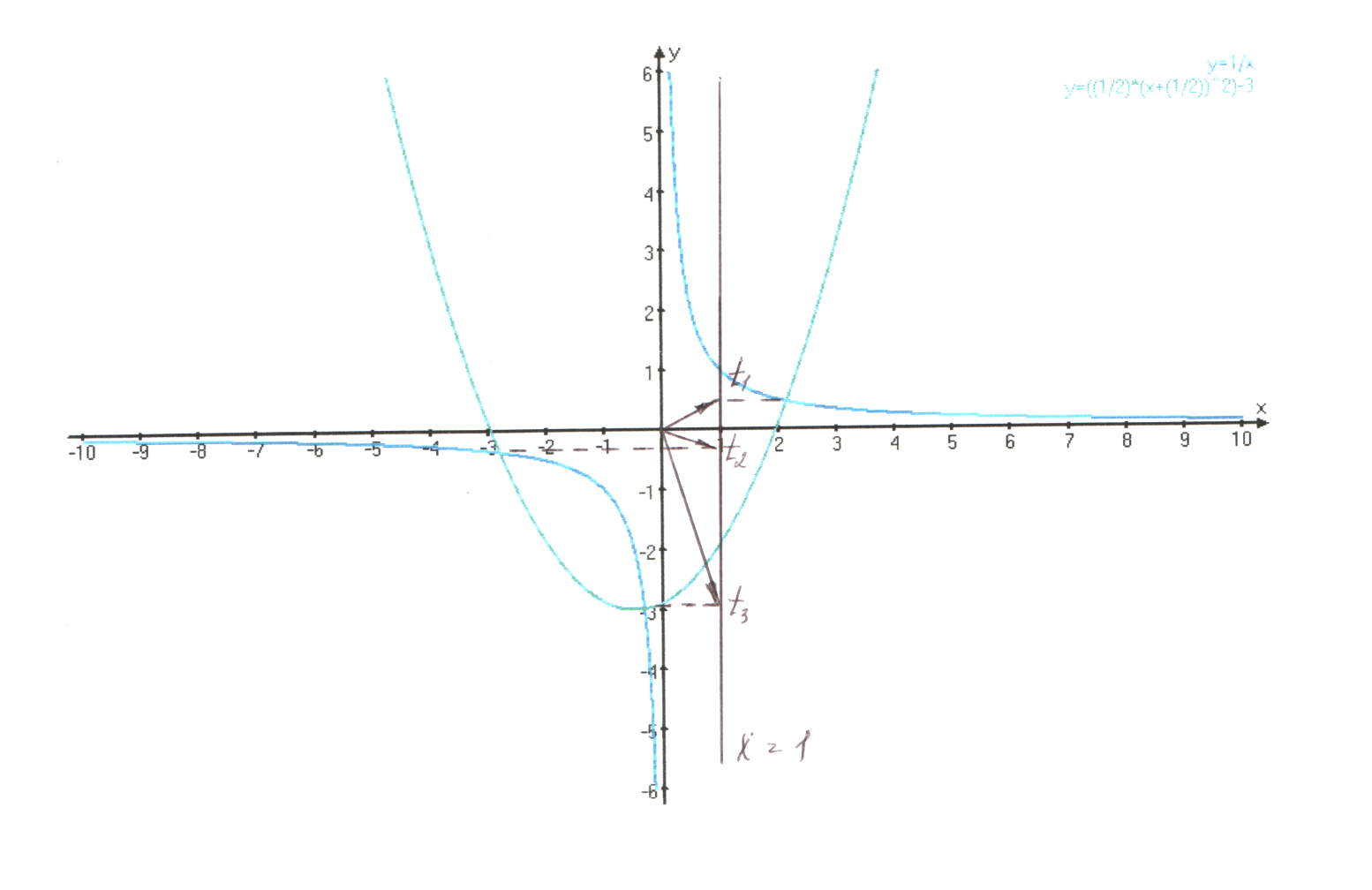
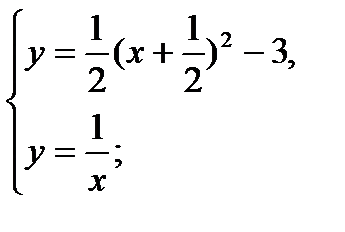
Рис. 9
Графическое решение системы показано на рис. 9
По рис. 9 находим: α 1 ≈ 25°, α 2 ≈ -20°, α 3 ≈ -71°.С учетом периодичности: t1 = 25° + 360°n; t2 = -20° + 360°k; t3 = -71° + 360°m, где n, k, m  Z.
Z.