
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Графический метод решения тригонометрических неравенств
|
|
Пример 8. Решите неравенство:
8cos3 t – 14cos2 t + 6cos t – 2sin2 t + 8sin t – 3 ≥ 0
Заменим sin2 t = 1 – cos2 t.
8cos3 t – 14cos2 t + 6cos t – 2 + 2cos2 t + 8sin t – 3 ≥ 0
8cos3 t – 12cos2 t + 6cos t + 8sin t – 5 ≥ 0
Пусть sin t = y, cos t = x
8x3 – 12x2 + 6x + 8y – 5 ≥ 0
8y ≥ -8x3 + 12x2 – 6x + 5
y ≥ -x3 +  x2 -
x2 - 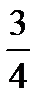 x +
x + 
y ≥ -(x3 -  x2 +
x2 + 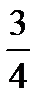 x -
x -  )
)
y ≥ -((x3 – 3∙ x2∙ 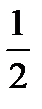 + 3∙ x∙
+ 3∙ x∙  -
- 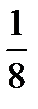 ) +
) + 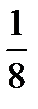 -
- 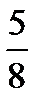 )
)
y ≥ -((x - 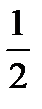 )3 -
)3 - 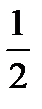 )
)
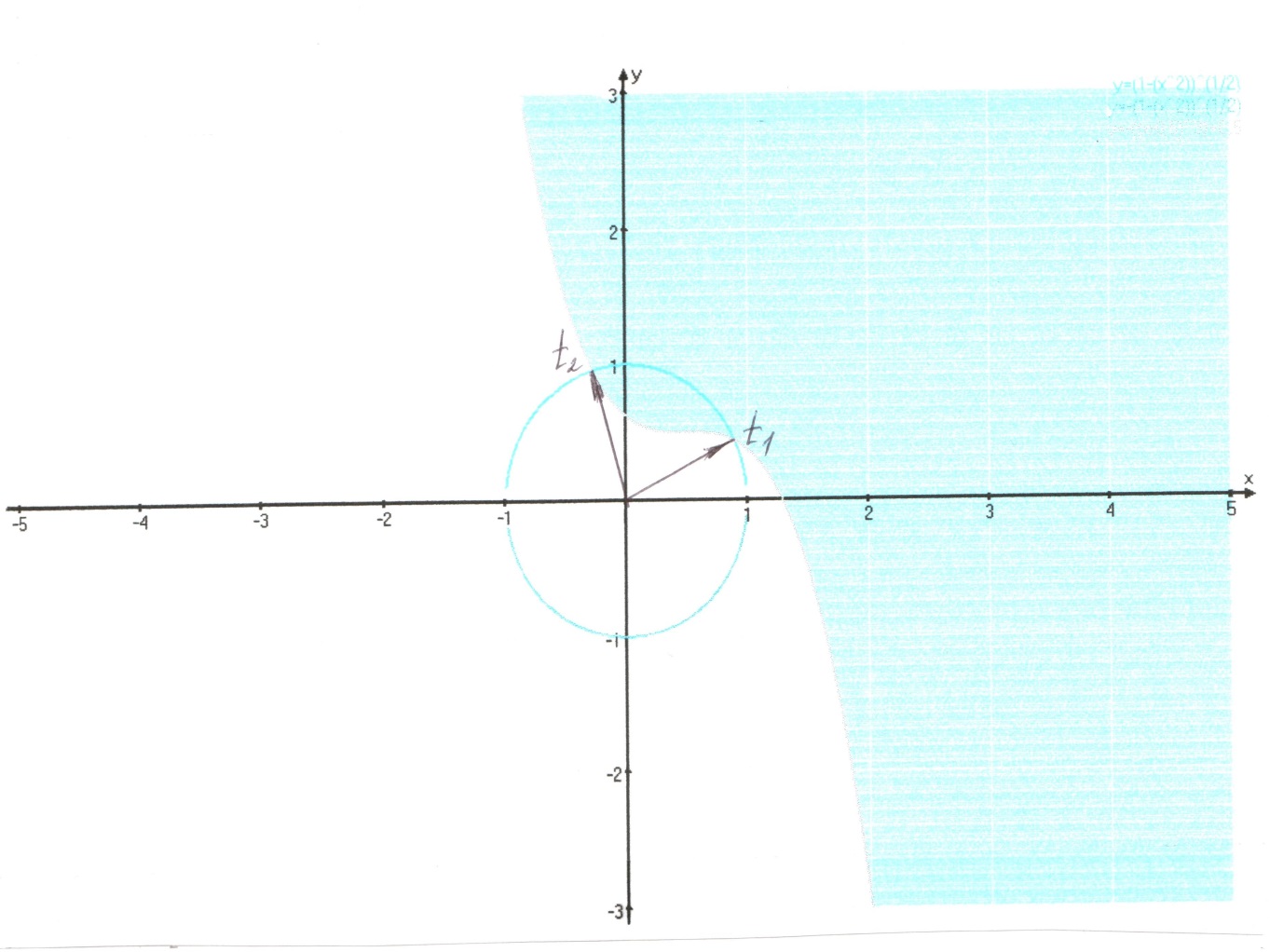 Остается решить графически систему, состоящую из неравенства (3) и из уравнения x2 + y2 = 1.
Остается решить графически систему, состоящую из неравенства (3) и из уравнения x2 + y2 = 1.

Рис. 10
Выделенная на рис. 10 дуга единичной окружности и является графическим решением этой вспомогательной системы.
Каждая точка этой дуг имеет радиус-вектор, образующий с положительным направлением оси Ox угол, величина которого изменяется в промежутке [26°; 106°]. Учитывая периодичность, получаем t  [26°+ 360°k; 106°+360°k], где k
[26°+ 360°k; 106°+360°k], где k  Z.
Z.
Пример 9. Решите неравенство: 2tg t + ctg2 t – 2ctg t – 4 < 0
Введем обозначения и приведем неравенство к виду, удобному для построения графика:
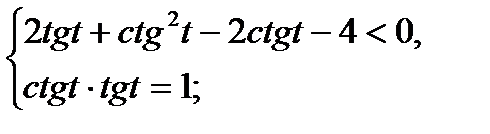
Преобразуем первое уравнение системы:
2y + x2 – 2x – 4 < 0
2y < - x2 + 2x + 4
y < - 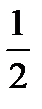 x2 + x + 2
x2 + x + 2
y < - 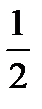 (x2 – 2x – 4)
(x2 – 2x – 4)
y < - 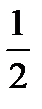 ((x2 – 2x + 1) – 1 – 4)
((x2 – 2x + 1) – 1 – 4)
y < - 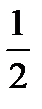 ((x – 2)2 – 5)
((x – 2)2 – 5)

Решим графически систему, состоящую из неравенства(4) и уравнения
xy = 1.
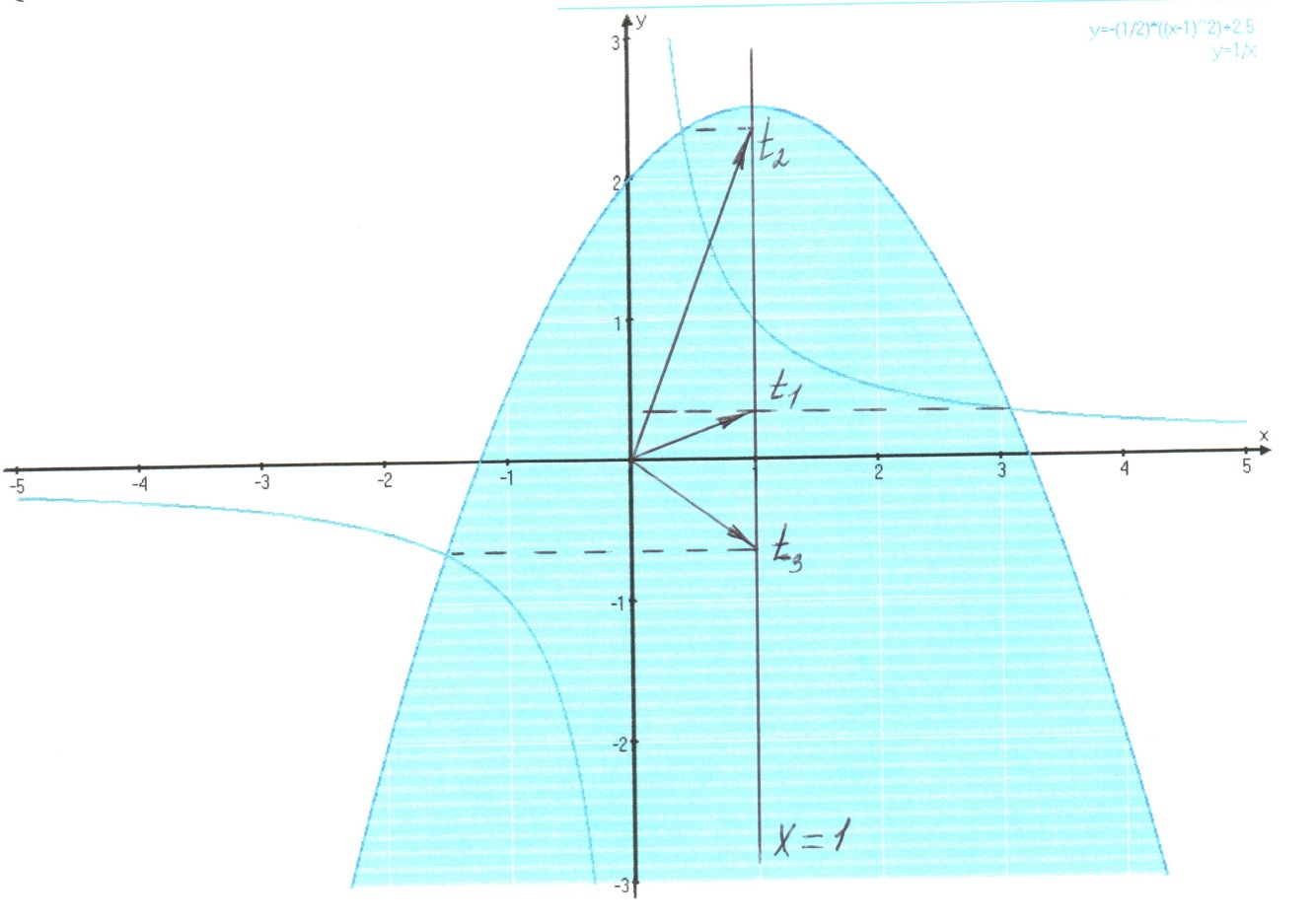
Рис. 11
Этой системе удовлетворяют координаты точек, выделенных на гиперболе (рис. 11):
t  [-90°; t3],
[-90°; t3],
t  [t1; t2].
[t1; t2].
Вспомним теперь о введении первоначального обозначения y = tg t и выделим на оси тангенсов промежутки, состоящие из точек, чьи ординаты такие же, как и ординаты пунктирной части гиперболы.
Углы, которые составляют радиус-векторы точек, лежащих на отрезке AB и на луче CE линии тангенсов, и является решением исходного неравенства, т.е. t  [-90°; -33°] или t
[-90°; -33°] или t  [18°; 67°].
[18°; 67°].
При записи окончательного ответа следует учесть периодичность:
t  [-90° + 180°k; -33° + 180°k] или
[-90° + 180°k; -33° + 180°k] или
t  [18° + 180°n; 67° + 180°n], n, k
[18° + 180°n; 67° + 180°n], n, k  Z.
Z.
В заключение приведем ряд уравнений и неравенств, которые удобно решать рассмотренным методом:
1) sin t + 2cos2 t – 4cos t – 1 = 0
2) 2sin t + cos3 t = 1
3) 2tg t – ctg3 t = 2
4) cos t – 2sin t – 1 = 0
5) sin t + 1 < 2-1 e cos t
6) 4sn t + 2cos3 t ≤ 1
7) tg t + 1 = 2ctg t + 1
8) sin t – 2sin2 (2cos t) > 0
Гармонические колебания и их характеристики
Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени. Колебания широко распространены в окружающем мире и могут иметь самую различную природу. Это могут быть механические (маятник), электромагнитные (колебательный контур) и другие виды колебаний.
Свободными, или собственными колебаниями, называются колебания, которые происходят в системе предоставленной самой себе, после того как она была выведена внешним воздействием из состояния равновесия. Примером могут служить колебания шарика, подвешенного на нити. (ПРИМЕРЫ )
)
Особую роль в колебательных процессах имеет простейший вид колебаний - гармонические колебания. Гармонические колебания лежат в основе единого подхода при изучении колебаний различной природы, так как колебания, встречающиеся в природе и технике, часто близки к гармоническим, а периодические процессы иной формы можно представить как наложение гармонических колебаний.
Гармоническими колебаниями называются такие колебания, при которых колеблющаяся величина меняется от времени по закону синуса или косинуса.
Уравнение гармонических колебаний имеет вид:
 ,
,
где A - амплитуда колебаний (величина наибольшего отклонения системы от положения равновесия); 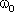 - круговая (циклическая) частота. Периодически изменяющийся аргумент косинуса
- круговая (циклическая) частота. Периодически изменяющийся аргумент косинуса  - называется фазой колебаний. Фаза колебаний определяет смещение колеблющейся величины от положения равновесия в данный момент времени t. Постоянная φ представляет собой значение фазы в момент времени t = 0 и называется начальной фазой колебания. Значение начальной фазы определяется выбором начала отсчета. Величина x может принимать значения, лежащие в пределах от -A до +A.
- называется фазой колебаний. Фаза колебаний определяет смещение колеблющейся величины от положения равновесия в данный момент времени t. Постоянная φ представляет собой значение фазы в момент времени t = 0 и называется начальной фазой колебания. Значение начальной фазы определяется выбором начала отсчета. Величина x может принимать значения, лежащие в пределах от -A до +A.
Промежуток времени T, через который повторяются определенные состояния колебательной системы, называется периодом колебаний. Косинус - периодическая функция с периодом 2π, поэтому за промежуток времени T, через который фаза колебаний получит приращение равное 2π, состояние системы, совершающей гармонические колебания, будет повторяться. Этот промежуток времени T называется периодом гармонических колебаний.
Период гармонических колебаний равен: T = 2π / 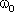 .
.
Число колебаний в единицу времени называется частотой колебаний ν.
Частота гармонических колебаний равна: ν = 1/T. Единица измерения частоты герц (Гц) - одно колебание в секунду.
Круговая частота 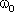 = 2π /T = 2π ν дает число колебаний за 2π секунд.
= 2π /T = 2π ν дает число колебаний за 2π секунд.
Графически гармонические колебания можно изображать в виде зависимости x от t (рис.1.1.А), так и методом вращающейся амплитуды (метод векторных диаграмм) (рис.1.1.Б). (ПРИМЕР )
)

|
| Рисунок 1.1. Графическое изображение гармонических колебаний |
Метод вращающейся амплитуды позволяет наглядно представить все параметры, входящие в уравнение гармонических колебаний. Действительно, если вектор амплитуды А расположен под углом φ к оси х (см. Рисунок 1.1. Б), то его проекция на ось х будет равна: x = Acos(φ). Угол φ и есть начальная фаза. Если вектор А привести во вращение с угловой скоростью 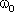 , равной круговой частоте колебаний, то проекция конца вектора будет перемещаться по оси х и принимать значения, лежащие в пределах от -A до +A, причем координата этой проекции будет меняться со временем по закону:
, равной круговой частоте колебаний, то проекция конца вектора будет перемещаться по оси х и принимать значения, лежащие в пределах от -A до +A, причем координата этой проекции будет меняться со временем по закону:
 .
.
Таким образом, длина вектора равна амплитуде гармонического колебания, направление вектора в начальный момент образует с осью x угол равный начальной фазе колебаний φ, а изменение угла направления от времени равно фазе гармонических колебаний. Время, за которое вектор амплитуды делает один полный оборот, равно периоду Т гармонических колебаний. Число оборотов вектора в секунду равно частоте колебаний ν.
Сложение двух гармонических колебаний одинакового направления и частоты
При сложении двух гармонических колебаний одинакового направления и частоты, результирующее смещение будет суммой ( ) смещений
) смещений 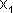 и
и 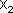 , которые запишутся следующими выражениями:
, которые запишутся следующими выражениями:
 ,
, 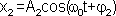 ,
,
Сумма двух гармонических колебаний также будет гармоническим колебанием той же круговой частоты:
 =
=  .
.
Значения амплитуды А и начальной фазы φ этого гармонического колебания будет зависеть от амплитуд исходных колебаний и их начальных фаз (Рис. 1.2).
|
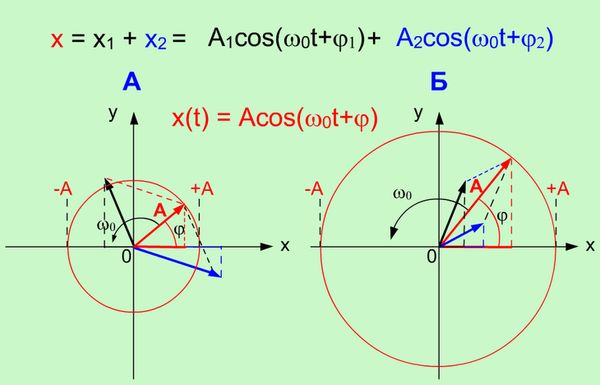
| Рисунок 1.2. Сложение двух гармонических колебаний одинакового направления и частоты |
На рисунке 1.2. приведено два примера А и В сложения гармонических колебаний с использованием метода векторных диаграмм. Из векторных диаграмм видно, что направление (начальная фаза φ) и длина А вектора амплитуды суммарного гармонического колебания зависит, как от направления (от начальных фаз), так и от длины векторов амплитуд исходных гармонических колебаний.
Если угол (разность фаз: Δ φ = φ 1 - φ 2) между векторами А1 и А2 равен 0, то исходные колебания находятся в фазе и суммарная амплитуда (А =А1 +А2) будет максимальна. Если угол (разность фаз: Δ φ = φ 1 - φ 2) между векторами А1 и А2 равен - π или π, то исходные колебания находятся в противофазе и суммарная амплитуда (А =  А1 -А2
А1 -А2  ) будет минимальна.(ПРИМЕР
) будет минимальна.(ПРИМЕР )
)
Сложение двух гармонических колебаний с неодинаковыми частотами.
(Биения и модуляции)
Если частоты колебаний 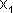 и
и 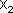 , неодинаковы, векторы А1 и А2 будут вращаться с различной скоростью. В этом случае результирующий вектор А пульсирует по величине и вращается с не постоянной скоростью. Результирующим движение уже будет не гармоническое колебание, а сложный колебательный процесс.
, неодинаковы, векторы А1 и А2 будут вращаться с различной скоростью. В этом случае результирующий вектор А пульсирует по величине и вращается с не постоянной скоростью. Результирующим движение уже будет не гармоническое колебание, а сложный колебательный процесс.
Биения
Биения возникают при сложении колебаний, отличающихся по частоте на небольшую величину, и проявляются в появлении более низкочастотных изменений амплитуды суммарного сигнала, по сравнению с исходными частотами. Амплитуда колебаний при этом меняется от минимального значения равного разности исходных амплитуд до максимального значения, равного сумме амплитуд исходных колебаний, и вновь до минимального значения. Периодом биений является время повторения этого процесса (Рис 1.3.).

|
| Рисунок 1.3. Биения |
За счет того, что вращение векторов А1 и А2 происходит с близкими, но отличающимися скоростями, разность фаз этих двух колебаний будет не постоянна, а медленно, то увеличиваться, то уменьшаться. Колебания будут находиться, то в фазе, то в противофазе, в результате амплитуда суммарного сигнала тоже будет меняться. Время за которое разность фаз измениться на 2π и будет периодом биений Тб (Тб = 2π /Δ ω). Δ ω -разность круговых частот исходных колебаний.
Биения применяют при обнаружении металлических предметов мин, оружия и т.д. Для этого используют два одинаковых высокочастотных колебательных контура, имеющих одинаковую частоту. Если вблизи одного из них появится металлический предмет, частота этого контура немного изменится. При сложении сигналов от этих двух контуров, в суммарном сигнале возникнет низкочастотная составляющая. Ее можно выделить и подать в наушники, в которых возникнут звуковые колебания, сигнализирующие о наличии металлического предмета.