Тангенс

Тангенсом числа называется отношение синуса этого числа к косинусу этого числа: .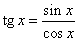

Тангенсом угла в а радиан называется тангенс числа а.

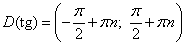Тангенс - функция числа. Ее область определения - множество всех чисел, у которых косинус не равен нулю, так как никаких других ограничений в определении тангенса нет. И так как косинус равен нулю при , то , где .

Область значений тангенса - множество всех действительных чисел.

Период тангенса равен . Ведь если взять любые два допустимые значения x (не равные 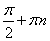), отличающиеся друг от друга на , и провести через них прямую, то эта прямая пройдет через начало координат и пересечет линию тангенсов в некоторой точке t. Вот и получится, что 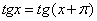, то есть число является периодом тангенса.

Знак тангенса: тангенс - отношение синуса к косинусу. Значит, он

1. равен нулю, когда синус равен нулю, то есть при , где n - любое целое число.

2. положителен, когда синус и косинус имеют одинаковые знаки. Это бывает только в первой и в третьей четвертях, то есть при 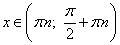, где а - любое целое число.

3. отрицателен, когда синус и косинус имеют разные знаки. Это бывает только во второй и в четвертой четвертях, то есть при , где а - любое целое число.

Тангенс - функция нечетная. Во-первых, область определения этой функции симметрична относительно начала отсчета. А во-вторых, . В силу нечетности синуса и четности косинуса, числитель полученной дроби равен , а ее знаменатель равен , а значит, сама эта дробь равна .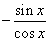

Вот и получилось, что .

Значит, тангенс возрастает на каждом участке своей области определения, то есть на всех интервалах вида 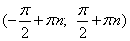, где а - любое целое число.