
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Параллельность плоскостей - признак и условия параллельности.
|
|
При решении геометрических задач часто встает вопрос: «параллельны ли две заданные плоскости»? Для ответа на него существует признак параллельности плоскостей, который представляет собой достаточное условие параллельности плоскостей. Сформулируем его в виде теоремы.
Теорема.
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым, лежащим в другой плоскости, то такие плоскости параллельны.
С доказательством этого признака параллельности плоскостей Вы можете ознакомиться на страницах учебника геометрии за 10 - 11 классы, который указан в конце статьи в списке рекомендованной литературы.
На практике для доказательства параллельности плоскостей также часто используются две следующие теоремы.
Теорема.
Если одна из двух параллельных плоскостей параллельна третьей плоскости, то другая плоскость либо тоже параллельна этой плоскости, либо совпадает с ней.
Теорема.
Если две несовпадающие плоскости перпендикулярны некоторой прямой, то они параллельны.
На основании приведенных теорем и признака параллельности плоскостей доказывается параллельность любых двух плоскостей.
Теперь подробно остановимся на необходимом и достаточном условии параллельности двух плоскостей  и
и  , которые заданы в прямоугольной системе координат в трехмерном пространстве.
, которые заданы в прямоугольной системе координат в трехмерном пространстве.
Пусть в прямоугольной системе координат Oxyz плоскости  соответствует общее уравнение плоскости вида
соответствует общее уравнение плоскости вида 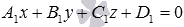 , а плоскости
, а плоскости  - вида
- вида 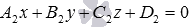 . (Если плоскости заданы уравнениями плоскостей в отрезках, то от них легко перейти к общим уравнениям плоскостей.)
. (Если плоскости заданы уравнениями плоскостей в отрезках, то от них легко перейти к общим уравнениям плоскостей.)
Теорема.
Для параллельности плоскостей  и
и  необходимо и достаточно, чтобы система линейных уравнений вида
необходимо и достаточно, чтобы система линейных уравнений вида  не имела решений (была несовместна).
не имела решений (была несовместна).
Доказательство.
Если плоскости 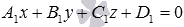 и
и 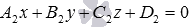 параллельны, то по определению они не имеют общих точек. Следовательно, не существует ни одной точки в прямоугольной системе координат Oxyz в трехмерном пространстве, координаты которой удовлетворяли бы одновременно обоим уравнениям плоскостей. Поэтому, система уравнений
параллельны, то по определению они не имеют общих точек. Следовательно, не существует ни одной точки в прямоугольной системе координат Oxyz в трехмерном пространстве, координаты которой удовлетворяли бы одновременно обоим уравнениям плоскостей. Поэтому, система уравнений  не имеет решений.
не имеет решений.
Если система линейных уравнений  не имеет решений, то не существует ни одной точки в прямоугольной системе координат Oxyz в трехмерном пространстве, координаты которой удовлетворяют одновременно обоим уравнениям системы. Следовательно, плоскости
не имеет решений, то не существует ни одной точки в прямоугольной системе координат Oxyz в трехмерном пространстве, координаты которой удовлетворяют одновременно обоим уравнениям системы. Следовательно, плоскости 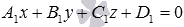 и
и 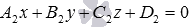 не имеют ни одной общей точки, то есть, они параллельны.
не имеют ни одной общей точки, то есть, они параллельны.
Рассмотрим применение необходимого и достаточного условия параллельности плоскостей.
Пример.
Параллельны ли плоскости 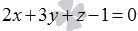 и
и  ?
?
Решение.
Составим систему уравнений из заданных уравнений плоскостей. Она имеет вид 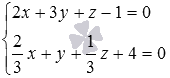 . Выясним, имеет ли эта система линейных уравнений решения (при необходимости смотрите статью решение систем линейных алгебраических уравнений).
. Выясним, имеет ли эта система линейных уравнений решения (при необходимости смотрите статью решение систем линейных алгебраических уравнений).
Ранг матрицы  равен одному, так как все миноры второго порядка равны нулю. Ранг матрицы
равен одному, так как все миноры второго порядка равны нулю. Ранг матрицы 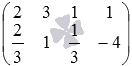 равен двум, так как минор
равен двум, так как минор 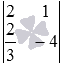 отличен от нуля. Итак, ранг основной матрицы системы уравнений меньше ранга расширенной матрицы системы. При этом из теоремы Кронекера-Капелли следует, что система уравнений
отличен от нуля. Итак, ранг основной матрицы системы уравнений меньше ранга расширенной матрицы системы. При этом из теоремы Кронекера-Капелли следует, что система уравнений 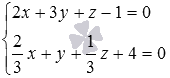 не имеет решений. Этим доказано, что плоскости
не имеет решений. Этим доказано, что плоскости 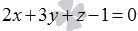 и
и  параллельны.
параллельны.
Заметим, что использование метода Гаусса для решения системы линейных уравнений 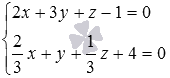 привело бы нас к этому же результату.
привело бы нас к этому же результату.
Ответ:
плоскости параллельны.
Необходимое и достаточное условие параллельности плоскостей можно сформулировать иначе.
Теорема.
Для параллельности двух несовпадающих плоскостей  и
и  необходимо и достаточно, чтобы нормальный вектор плоскости
необходимо и достаточно, чтобы нормальный вектор плоскости  и нормальный вектор плоскости
и нормальный вектор плоскости  были коллинеарны.
были коллинеарны.
Доказательство этого условия основано на определении нормального вектора плоскости.
Пусть 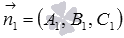 и
и  - нормальные векторы плоскостей
- нормальные векторы плоскостей  и
и  соответственно. Условие коллинеарности векторов
соответственно. Условие коллинеарности векторов 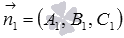 и
и  записывается как
записывается как  , где t – некоторое действительное число.
, где t – некоторое действительное число.
Таким образом, для параллельности несовпадающих плоскостей  и
и  , нормальными векторами которых являются векторы
, нормальными векторами которых являются векторы 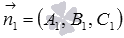 и
и  соответственно, необходимо и достаточно, чтобы существовало действительное число t, для которого справедливо равенство
соответственно, необходимо и достаточно, чтобы существовало действительное число t, для которого справедливо равенство  .
.
Пример.
Известно, что в прямоугольной системе координат Oxyz в трехмерном пространстве плоскость  проходит через три точки
проходит через три точки 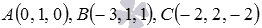 , а плоскость
, а плоскость  определяется уравнением
определяется уравнением  . Докажите параллельность плоскостей
. Докажите параллельность плоскостей  и
и  .
.
Решение.
Сначала убедимся, что плоскости  и
и  не совпадают. Это действительно так, так как координаты точки А не удовлетворяют уравнению плоскости
не совпадают. Это действительно так, так как координаты точки А не удовлетворяют уравнению плоскости  .
.
Теперь найдем координаты нормальных векторов 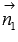 и
и 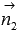 плоскостей
плоскостей  и
и  и проверим выполнение условия коллинеарности векторов
и проверим выполнение условия коллинеарности векторов 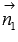 и
и 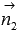 .
.
В качестве вектора 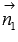 можно взять векторное произведение векторов
можно взять векторное произведение векторов  и
и  . Векторы
. Векторы  и
и  имеют координаты
имеют координаты  и
и  соответственно (при необходимости смотрите статью нахождение координат вектора по координатам точек его начала и конца). Тогда
соответственно (при необходимости смотрите статью нахождение координат вектора по координатам точек его начала и конца). Тогда 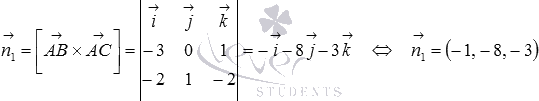 .
.
Чтобы определить координаты нормального вектора плоскости  приведем ее уравнение к общему уравнению плоскости:
приведем ее уравнение к общему уравнению плоскости: 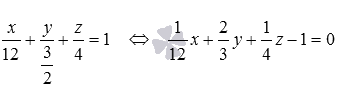 . Теперь видно, что
. Теперь видно, что 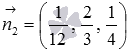 .
.
Проверим выполнение условия коллинеарности векторов 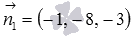 и
и 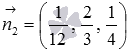 .
.
Так как 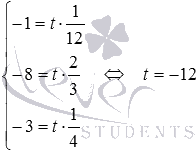 , то векторы
, то векторы 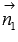 и
и 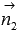 связаны равенством
связаны равенством  , то есть, они коллинеарны.
, то есть, они коллинеарны.
Итак, плоскости  и
и  не совпадают, а их нормальные векторы коллинеарны, следовательно, плоскости
не совпадают, а их нормальные векторы коллинеарны, следовательно, плоскости  и
и  параллельны.
параллельны.
Замечание: разобранное необходимое и достаточное условие не очень удобно для доказательства параллельности плоскостей, так как отдельно приходится доказывать, что плоскости не совпадают.