Определение

Вектор, длина которого равна единице, называется единичным вектором или ортом.

Векторы называются равными, если они лежат на одной или параллельных прямых; их направления совпадают и длины равны.

Иначе говоря, два вектора равны, если они коллинеарны, сонаправлены и имеют равные длины:

, если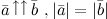

В произвольной точке пространства можно построить единственный вектор , равный заданному вектору .

Правило параллелограмма сложение векторных величин, сумма нескольких векторов. Произведение вектора на число. Такой приём сложения нескольких векторов называется правилом многоугольника. Сочетательный закон сложения векторов. Суммы нескольких векторов, правилом многоугольника ознакомить учащихся со свойством сложения нескольких векторов. Правило многоугольника или правило цепи. Из закона следует, что сумма не зависит от того, в каком порядке они.. Сумма нескольких векторов, Правило параллелепипеда. Сумма нескольких векторов (правило многоугольника). Суммой векторов = и = называется вектор = + = + =. Ученик (114), на голосовании 1 год назад 1 год назад. В чём заключается правило многоугольника сложения нескольких векторов? Александр Попиков Ученик (60), закрыт 3 года назад 3 года назад.

Метод координат — способ определять положение точки или тела с помощью чисел или других символов (например, положение шахматных фигур на доске определяется с помощью чисел и букв). Числа (символы), определяющие положение точки (тела) на прямой, плоскости, в пространстве, на поверхности и так далее, называются её координатами. В зависимости от целей и характера исследования выбирают различные системы координат.

ДЕКАРТОВА СИСТЕМА КООРДИНАТ, система, введенная Рене ДЕКАРТОМ, в которой положение точки определяется расстоянием от нее до взаимно пересекающихся линий (осей). В простейшем варианте системы оси (которые обозначаются как х и у) перпендикулярны. Положение точки задается парой чисел (х, у). Абсцисса, х, -это расстояние от точки до оси у, измеренное в направлении оси х; ордината, у, -это расстояние до оси х. Оси в этой системе не обязательно должны пересекаться под прямым углом, однако, и не должны быть параллельны одна другой. Для описания позиции точки в трехмерном пространстве необходимы три оси.