
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Активности
|
|
Методом ЭДС можно определить средние ионные коэффициенты активности.
Способ 1− расчетный. Для этой цели используются элементы без переноса. Пусть необходимо определить 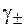 в водном растворе HBr с концентрацией
в водном растворе HBr с концентрацией 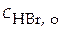 . Составляем гальванический элемент без переноса, схема которого
. Составляем гальванический элемент без переноса, схема которого
Pt (H2) | HBr | AgBrтв, Ag| Pt
Известно, что  ,
, 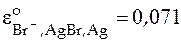 В.
В.
Уравнения электродных реакций:
H2 - 2e + 2H2O = 2 H3O+
AgBr + e = Ag + Br-
Итоговая реакция: H2+ 2H2O + 2AgBr = 2H3O+ + 2Ag + 2 Br-
Запишем уравнение Нернста для данной суммарной реакции, протекающей в гальваническом элементе:
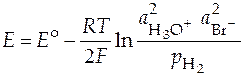 .
.
При давлении 1 атм это выражение упрощается:
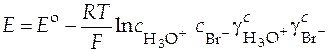 .
.
Реакция HBr + H2O = H3O+ + Br- идет практически до конца, т.е. 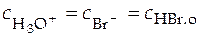 , а
, а 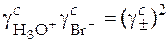 .
.
Следовательно,
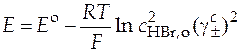 .
.
Отсюда логарифм среднего ионного коэффициента активности равен
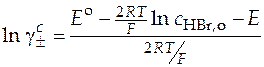 . (42)
. (42)
По формуле (42) нетрудно вычислить значение среднего ионного коэффициента активности, располагая данными о начальной концентрации кислоты и о значениях стандартных условных электродных потенциалов. Следует отметить, что эти значения (стандартных электродных потенциалов) приводятся в справочниках при температуре растворов 298 К.
Способ 2 –графический. Если необходимо вычислить коэффициенты активности при другой, отличной от 298 К температуре, поступают следующим образом. Составляют гальванический элемент без переноса, например такой
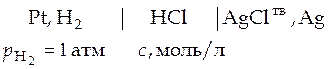
Проводят серию опытов, в которых измеряют ЭДС такого гальванического элемента, но концентрация электролита в каждом опыте разная. Эта концентрация задается исследователем, т.е. она известна. Например, электродвижущая сила (Е, В) указанного гальванического элемента была измерена при температуре 313 К в серии опытов с различными значениями концентрации соляной кислоты 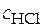 , моль/л.
, моль/л.
Как найти по этим данным величину среднего ионного коэффициента активности в растворе соляной кислоты какой-либо концентрации, например, 0, 023 моль/л.
При температуре 313 К в справочниках нет данных о значениях стандартных электродных потенциалов, поэтому величину стандартной ЭДС необходимо находить графически.
Уравнение Нернста для итоговой реакции, протекающей в данном гальваническом элементе будет иметь вид (14):
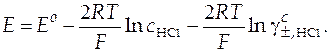
Запишем уравнение в виде, удобном для дальнейших расчетов:
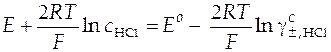 . (43)
. (43)
Слева в уравнении (43) находятся заданные по условию эксперимента (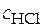 ) и измеренные в эксперименте величины (E). То, что расположено справа в уравнении, содержит две неизвестные величины − стандартную ЭДС (Eо) и средний ионный коэффициент активности в растворе хлорида водорода, который и нужно определить (
) и измеренные в эксперименте величины (E). То, что расположено справа в уравнении, содержит две неизвестные величины − стандартную ЭДС (Eо) и средний ионный коэффициент активности в растворе хлорида водорода, который и нужно определить (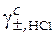 ).
).
Существует способ, который позволяет в определенных условиях сделать в правой части уравнения не две неизвестные величины, а одну. Если рассмотреть такое состояние, при котором средний ионный коэффициент активности в растворе электролита можно принять равным единице, то логарифм его будет равен нулю и тогда в правой части уравнения будет только одна неизвестная − стандартная ЭДС гальванического элемента при температуре исследования.
Известно, что средние ионные коэффициенты активности стремятся к единице в сильноразбавленных растворах, когда концентрация равна 0. Как это следует из предельного закона теории Дебая-Хюккеля, логарифм среднего ионного коэффициента активности пропорционален корню квадратному из величины ионной силы раствора (или корню квадратному концентрации электролита). Именно поэтому при графическом методе нахождения стандартной ЭДС гальванического элемента строят зависимость левой части уравнения (30) от корня квадратного из концентрации раствора электролита (рис.12).
 Нанеся экспериментальные значения
Нанеся экспериментальные значения 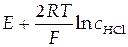 при разных значениях
при разных значениях 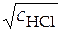 на график, получают зависимость, которую затем экстраполируют на нулевое значение
на график, получают зависимость, которую затем экстраполируют на нулевое значение 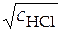 . Так находят стандартную ЭДС гальванического элемента при температуре, отличной от 298 К.
. Так находят стандартную ЭДС гальванического элемента при температуре, отличной от 298 К.
Затем возвращаются к уравнению (43). Вычисляют 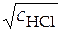 (т.е. корень квадратный из концентрации, при которой нужно найти средний ионный коэффициент активности − точка а на рис.12). По графику (рис.12) определяют значение
(т.е. корень квадратный из концентрации, при которой нужно найти средний ионный коэффициент активности − точка а на рис.12). По графику (рис.12) определяют значение 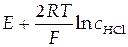 (точка b на рис.12). Зная
(точка b на рис.12). Зная 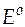 , по уравнению (43) нетрудно рассчитать и требуемую величину среднего ионного коэффициента активности.
, по уравнению (43) нетрудно рассчитать и требуемую величину среднего ионного коэффициента активности.
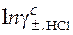
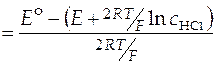 . (44)
. (44)
Для сравнения определенных экспериментально средних ионных коэффициентов активности с рассчитанными по теории Дебая-Хюккеля воспользуемся формулами предельного закона теории и второго приближения этой теории.
В случае предельного закона теории Дебая-Хюккеля
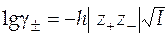 , (45)
, (45)
где 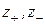 - заряды катиона и аниона;
- заряды катиона и аниона;
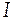 - ионная сила раствора;
- ионная сила раствора;
 - константа зависящая от диэлектрической проницаемости растворителя и температуры.
- константа зависящая от диэлектрической проницаемости растворителя и температуры.
Для водных растворов при разных температурах величина константы h равна:
Температура, К 298 303 313 323 Константа h, (л/моль)0, 5 0, 512 0, 517 0, 528 0, 539
Уравнение (45) справедливо до ионной силы 0, 01 моль/л.
Второе приближение теории Дебая-Хюккеля выражается следующим уравнением
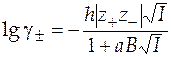 ,
,
где 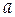 - расстояние наибольшего сближения электрических центров ионов;
- расстояние наибольшего сближения электрических центров ионов;
В – эмпирический параметр, зависящий от температуры.
Для водного раствора при 298 К В = 3, 29× 109 м-1× моль-0, 5кг0, 5.
Если принять расстояние наибольшего сближения равным 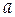 = 0, 304 нм, то можно вычислить средние коэффициенты активности по уравнению Гюнтельберга:
= 0, 304 нм, то можно вычислить средние коэффициенты активности по уравнению Гюнтельберга:
 . (46)
. (46)
Уравнение (46) справедливо до ионной силы 0, 1 моль/л.
ВАРИАНТЫ ЗАДАНИЙ НА КУРСОВУЮ РАБОТУ
В зависимости от подготовленности студентов и по усмотрению преподавателя полное задание на курсовую работу может включать в себя сочетание от двух до трех перечисленных далее вариантов фрагментов заданий.
Вариант А. Изложить теоретический материал по теме курсовой работы. Составить из предлагаемых электродов правильно разомкнутый гальванический элемент без переноса, записать электродные и итоговую реакции. Записать уравнение Нернста для ЭДС такого гальванического элемента.
Вариант В. Изложить теоретический материал и исследовать температурную зависимость ЭДС гальванического элемента. Рассчитать по данным ЭДС термодинамические характеристики реакции, протекающей в гальваническом элементе и сравнить их со справочными данными.
Вариант С. Изложить теоретический материал и на основании экспериментальных данных определить методом ЭДС средние ионные коэффициенты активности электролита исследуемого гальванического элемента и сравнить их с рассчитанными по теории Дебая-Хюккеля.
Вариант D. Изложить теоретический материал и определить величину константы ионизации слабой кислоты или слабого основания самостоятельно (или на основании приведенных в задании экспериментальных данных потенциометрического титрования). Сравнить полученные данные со справочными.
Вариант E. Изложить теоретический материал и определить самостоятельно (или на основании приведенных в задании экспериментальных данных) методом измерения ЭДС и рН-метрически величину константы ионизации слабой кислоты или слабого основания. Сравнить полученные данные со справочными.