Основы динамики электропривода

Поскольку периоды разгона и торможения электропривода не являются эффективным временем работы механизма, их длительность желательно по возможности сокращать, что особенно важно для привода механизмов, работающих с частыми пусками и остановками.

Продолжительность переходных процессов привода определяется интегрированием уравнения движения электропривода. Разделив переменные, получим для периода пуска

откуда

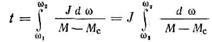
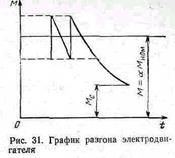
где J — момент инерции, приведенный к валу двигателя. Для решения этого интеграла необходимо знать зависимость моментов двигателя и механизма от скорости. Текущее значение момента двигателя при реостатном пуске заменим средним его значением М=α М_ном, как это показано на рис. 31. Тогда для простейшего случая пуска при условии, что M_c=const, получим следующее выражение для времени пуска от состояния покоя (ω ₁=0) до конечной угловой скорости (ω ₂= ω _ном), соответствующей статическому моменту М_c:

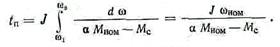
Время торможения определится из выражения

Из уравнения видно, что теоретически угловая скорость достигнет своего установившегося значения только через бесконеч­но большой промежуток времени (при t =∞). В практических же расчетах считают, что процесс разбега заканчивается при угловой скорости, равной не установившемуся ее значению ω = ω _с, а при ω =(0, 95÷ 0, 98)ω _с. Из уравнения следует, что уже при t= 3Т_м ω =0, 96 ω ₀, т. е. переходный процесс практически будет за­кончен за время t= (3÷ 4)T_м.

Поскольку пуск двигателей постоянного тока и асинхронных с фазным ротором часто осуществляется через многоступенчатый Реостат, необходимо уметь вычислять время разбега двигателя на каждой ступени.

Для ступени х уравнение может быть переписано в виде

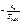
М = М_с + (М_к - М_с) е, (33)

где: М_к—номинальный момент при пуске; t_x — время разбега двигателя на рассматриваемой ступени; Т_мх — электромеханическая постоянная времени для этой же ступени.

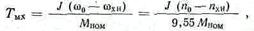
где ω _хн — угловая скорость на ступени х при М=М, ном.

Решая равенство (33) относительно времени пуска и учитывая равество (27), находим

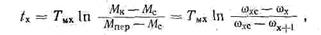
Где: ω _х—угловая скорость на ступени х при М=М_к; ω _х+1 —то же, на ступени х+ 1 при М=Мк; ω _хс — то же, на ступени х при M=М_с.

Время разбега на естественной характеристике te теоретически равно бесконечности. При расчетах же его принимают равным (3÷ 4)Т_м.е. Общее время разбега двигателя при пуске равно суммарному времени разбега на всех ступенях.

Время торможения электропривода определяется также реше-нием основного уравнения движения.

Замедление привода происходит в том случае, если динамический момент имеет отрицательное значение или когда вращающий момент двигателя меньше статического момента сопротивления

Для торможения противовключением, когда угловая скорость изменяется от ω = ω ₁ до ω =0, уравнение (27) может быть переписано в виде

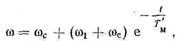
где

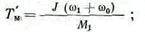
М₁ и ω ₁ — соответственно момент и угловая скорость двигателя в начале торможения; ω _с — угловая скорость, соответствующая моменту М_с на заданной механической характеристике.

Время торможения от ω ₁ до полной остановки составит

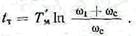
При динамическом торможении от w=w1 до w=0

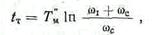
где

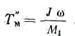
Время реверсирования можно рассматривать как сумму времени торможения и разбега в обратном направлении.

Основным уравнением, описывающим работу системы электро­привода, является уравнение движения. Пользуясь этим урав­нением, можно произвести анализ переходных процессов, вычислить время разгона и торможения, определить расход энергии и т. д.

Решив уравнение движения электроприводов относительно угловой скорости ω или вращающего момента двигателя М для про­стейшего случая, когда M_c = const, механическая характеристика двигателя линейна, получим уравнение переходного процесса при­вода

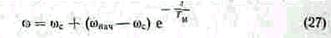
или

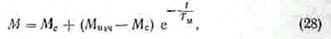
где M_с и ω _с — статический момент и соответствующая ему угловая скорость; Мнач и ω _нач — соответственно момент двигателя и угловая скорость в начале переходного режима; t — время, прошедшее от начала переходного режима; Т_м —электромеханическая постоянная чая времени.

Электромеханической постоянной называется время, в течение которого привод с приведенным моментом инерции J разгоняется вхолостую из неподвижного состояния до угловой скорости идеального холостого хода ω _о при неизменном вращающем моменте, равном моменту к.з. Мк (или начальному пусковому моменту) двигателя. С увеличением величины Т_м растет время переходных процессов и, как следствие, снижаются производительность и экономичность работы машины

Электромеханическая постоянная времени может быть определена ленаиз следующего выражения:

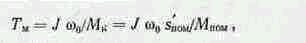
где: s_hom=(ω ₀—ω _ном)/ω _о—скольжение (для асинхронного двигателя) или относительный перепад скорости (для двигателя постоянного тока параллельного возбуждения) при работе на искусствен ной характеристике при номинальном моменте на валу двигателя; Mк —начальным пусковой момент двигателя (момент к.з.).

Из уравнении (27) и (28) следует, что при линейной механической характеристике двигателя и постоянном статическом моменте изменение угловой скорости и момента, развиваемого двигателем, происходит по экспоненциальному закону. В частном случае, когда пуск двигателя совершается под нагрузкой из неподвижного состояния (ω _нач=0), уравнение (27) принимает вид

и при пуске вхолостую, когда М_c= 0,

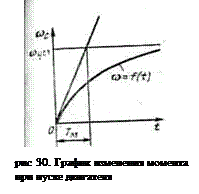
На рис. 30 изображен процесс нарастания угловой скорости движения согласно уравнению (27). Постоянная времени определяется из графика отрезком на прямой, отсекаемым касательной, проведенной из начала координат к кривой ω = f(t)

Лекция 7. Основы выбора электродвигателей.

В производственных условиях нагрузка на двигатель зависит от величины нагрузки механизма и характера изменения ее во времени.

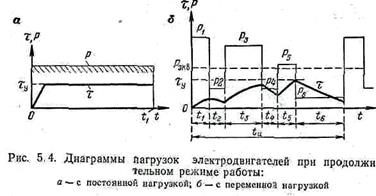
Закономерность изменения статической нагрузки во времени обычно.изображается в виде диаграмм, которые называются нагрузочными диаграммами механизма. На основании нагрузочных диаграмм механизма строятся нагрузочные диаграммы двигателя, в которых учитыва­ются статистические и динамические нагрузки.

Так как нагрев двигателей в основном происходит за счет потерь электроэнергии в обмотках двигателя, а при различных нагрузках величина тока в обмотках различна, то и температура

обмоток двигателя будет зависеть от нагрузочных диаграмм.

Нагрузочные диаграммы электродвигателей делятся:

по характеру изменений величины нагрузки во вре­мени — на диаграммы с постоянной и переменной на­грузкой (рис. 5.4);

по продолжительности нагрузки — на диаграммы с продолжительной, кратковременной, повторно-кратковре­менной и перемежающейся нагрузкой.

В соответствии с таким делением нагрузок принято различать четыре основных режима работы двигателей с постоянной и переменной нагрузкой: продолжительный, кратковременный, повторно-кратковременный, перемежа­ющийся.

В каждом двигателе имеются токоведущие части, изолированные изоляцией. Изоляция, не меняя своих параметров, выдерживает только определенную темпе­ратуру. Эта температура и есть пре­дельная (допустимая) температура, до которой может нагреваться двигатель. Если двигатель будет нагружен так, что его τ _у будет выше τ _д, — он выйдет из строя.

Конечная температура электродвигателя τ _н слагается из превышения его температуры над температурой окру­жающей среды и температуры окружающей среды (для средней полосы СССР она принята 308 К). Учитывая это положение, следует сделать вывод, что в характеристи­ках двигателей указана мощность для окружающей сре­ды с температурой 308 К. При изменении температуры окружающей среды можно, в определенных пределах, менять и нагрузку на двигатель против его паспортной мощности.

Допустимые температуры нагрева обмоток двигателей ограничиваются свойствами различных классов изоля­ции, а именно:

класс У, τ _д =363 К — непропитанные хлопчатобу­мажные ткани, пряжа, бумага и волокнистые материалы из целлюлозы и шелка;

класс А, τ _д = 378 К—те же материалы, но пропитан­ные жидким диэлектриком (маслом, лаком) или опущен­ные в трансформаторное масло;

класс Е, τ _д = 393 К—синтетические органические пленки, пластмассы (гетинакс, текстолит), изоляция эма­лированных проводов на основе лаков;

класс В, τ _д = 403 К—материалы из слюды, асбеста и стекловолокна, содержащие органические вещества (миканит, стеклоткань, стеклотекстолит) и некоторые пластмассы с минеральным наполнением;

класс F, τ _д = 428 К—те же материалы в сочетании с синтетическими связующими и пропитывающими веще­ствами повышенной теплостойкости;

класс Н, τ _д = 453 К—те же материалы в сочетании с кремнийорганическими связующими и пропитывающими веществами, а также кремнийорганическая резина;

класс С, τ _д более 453 К — слюда, электротехническая керамика, стекло, кварц, асбест, применяемые без свя­зующих составов или с неорганическими связующими со­ставами.