
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Система уравнений Максвелла для электромагнитного поля.
|
|
43. Вихревое электрическое поле.
Для объяснения возникновения индукционного тока в неподвижных проводниках {второй опыт Фарадея) Максвелл предположил, что всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в контуре (первое основное положение теории Максвелла).
Циркуляция вектора напряженности 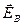 этого поля
этого поля
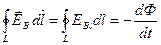
По определению поток вектора 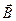 :
: 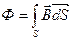 , откуда следует:
, откуда следует:
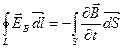
Здесь и в дальнейшем мы используем частную производной по времени, поскольку в общем случае электрическое поле может быть неоднородным, и может зависеть не только от времени, но и от координат.
Таким образом, циркуляция вектора 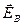 не равна нулю, т.е. электрическое поле
не равна нулю, т.е. электрическое поле 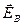 , возбуждаемое переменным магнитным полем, как и само магнитное поле, является вихревым.
, возбуждаемое переменным магнитным полем, как и само магнитное поле, является вихревым.
Суммарное электрическое поле складывается из электрического поля, создаваемого зарядами 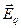 и вихревого электрического поля
и вихревого электрического поля 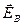 . Поскольку циркуляция
. Поскольку циркуляция 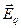 равна нулю, то циркуляция суммарного поля:
равна нулю, то циркуляция суммарного поля:
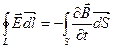
Это — первое уравнение системы уравнений Максвелла для электромагнитного поля.
44. Ток смещения.
Максвелл предположил, что аналогично магнитному полю и всякое изменение электрического поля вызывает в окружающем пространстве вихревое магнитное поле (второе основное положение теории Максвелла).
Поскольку магнитное поле есть основной, обязательный признак всякого тока, то Максвелл назвал переменное электрическое поле током смещения, в отличие от тока проводимости, обусловленного движением заряженных частиц.
Надо сказать, что термин ток смещения не является удачным. Он имеет некоторое основание в случае диэлектриков, так как в них действительно смещаются заряды в атомах и молекулах. Однако понятие тока смещения применяется и для полей в вакууме, где никаких зарядов, а следовательно и никакого их смещения нет. Тем не менее этот термин сохранился в силу исторических традиций.
Плотность тока смещения:
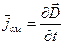
Следует подчеркнуть, что ток смещения определяется производной вектора 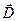 , но не самим вектором
, но не самим вектором 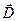 .Так например, в поле плоского конденсатора вектор
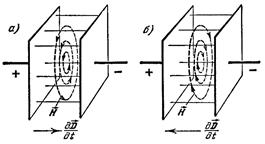
.Так например, в поле плоского конденсатора вектор 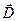 всегда направлен от положительной пластины к отрицательной. Но в случае, если электрическое поле возрастает, то
всегда направлен от положительной пластины к отрицательной. Но в случае, если электрическое поле возрастает, то  , а следовательно и ток смещения направлены так, как показано на рисунке (а). Если же электрическое поле убывает, то
, а следовательно и ток смещения направлены так, как показано на рисунке (а). Если же электрическое поле убывает, то  tа ктрическое поле положительной пластины к отрицательной. направлено от отрицательной пластины к положительной, и магнитное поле противоположно (рис. (б)) по сравнению с первым случаем.
tа ктрическое поле положительной пластины к отрицательной. направлено от отрицательной пластины к положительной, и магнитное поле противоположно (рис. (б)) по сравнению с первым случаем.
Если в каком-либо проводнике имеется переменный ток, то внутри проводника существует переменное электрическое поле. Поэтому внутри проводника имеется и ток проводимости, и ток смещения и магнитное поле проводника определяется суммой этих двух токов.
Максвелл ввел понятие полного тока, равного сумме токов проводимости и смещения. Плотность полного тока
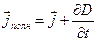
Полный ток всегда замкнут. На концах проводников обрывается лишь ток проводимости, а в диэлектрике (или в вакууме) между концами проводника имеется ток смещения, который замыкает ток проводимости.
Из всех физических свойств, присущих току проводимости, Максвелл приписал току смещения лишь одно — способность создавать в окружающем пространстве магнитное поле.
Максвелл обобщил теорему о циркуляции вектора НЛ использовав полный ток:

Обобщенная теорема о циркуляции вектора 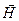 представляет собой второе уравнение системы уравнений Максвелла для электромагнитного поля.
представляет собой второе уравнение системы уравнений Максвелла для электромагнитного поля.
45. Полная система уравнений Максвелла.
Третье уравнение системы уравнений Максвелла для электромагнитного поля это теорема Гаусса для поля 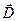 . Для заряда, непрерывно распределенного внутри замкнутой поверхности с объемной плотностью ρ, это уравнение имеет вид:
. Для заряда, непрерывно распределенного внутри замкнутой поверхности с объемной плотностью ρ, это уравнение имеет вид:

Четвертое уравнение Максвелла — это теорема Гаусса для поля 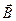 :
:

Таким образом, система уравнений Максвелла в интегральной форме
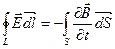 ;
;

 ;
;

Для того, чтобы эта система уравнений была полной ее необходимо дополнить такими соотношениями, в которые входили бы величины, характеризующие индивидуальные свойства среды, в которой возбуждаются электрические и магнитные поля. Эти соотношения называются материальными соотношениями:
 ,
, 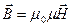 ,
, 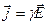
где 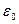 и
и 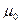 — соответственно электрическая и магнитная постоянные,
— соответственно электрическая и магнитная постоянные, 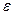 и μ — соответственно диэлектрическая и магнитная проницаемости, γ — удельная проводимость вещества.
и μ — соответственно диэлектрическая и магнитная проницаемости, γ — удельная проводимость вещества.
Из уравнений Максвелла следует, что
— источниками электрического поля являются либо электрические заряды, либо изменяющиеся во времени магнитные поля,
— магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями,
— переменное магнитное поле всегда связано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнитным, т.е. электрическое и магнитное поля неразрывно связаны друг с другом — они образуют единое электромагнитное поле.
Для стационарных полей (Е = const и В = const) уравнения Максвелла имеют вид
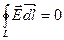 ;
;  ;
; 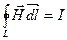 ;
; 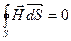 ;
;
В этом случае электрические и магнитные поля независимы друг от друга, что позволяет изучать отдельно постоянные электрическое и магнитное поле.
Воспользуемся известными из векторного анализа теоремами Стокса и Гаусса (см. стр.1-31):
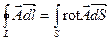
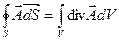
По определению, дивергенцией и ротором векторного поля А в данной точке Л/ называют следующие производные по объёму:
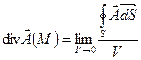
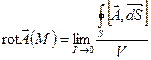
где интегралы 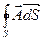 и
и 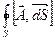 есть, соответственно, скалярный и векторный потоки векторного поля через замкнутую поверхность S, которая окружает данную точку М, охватывая область с объёмом V.
есть, соответственно, скалярный и векторный потоки векторного поля через замкнутую поверхность S, которая окружает данную точку М, охватывая область с объёмом V.
Дивергенция есть мера источников поля. Если в некоторой области дивергенция равна нулю, то векторное поле в этой области свободно от источников. Те точки поля, в которых дивергенция положительна, называются источниками поля, а в которых отрицательна — стоками векторного поля
Используя теоремы Стокса и Гаусса, можно представить полную систему уравнений Максвелла в дифференциальной форме (характеризующих поле в каждой точке пространства):
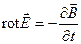
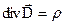


Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе существуют электрические заряды, но нет зарядов магнитных.
Так, например, уравнение 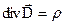 явно демонстрирует, что источниками электрического поля являются положительные электрические заряды, а стоками — отрицательные электрические заряды. Уравнение
явно демонстрирует, что источниками электрического поля являются положительные электрические заряды, а стоками — отрицательные электрические заряды. Уравнение  отражает тот факт, что не существует источников и стоков магнитного поля — " магнитных зарядов".
отражает тот факт, что не существует источников и стоков магнитного поля — " магнитных зарядов".
В случае если заряды и токи распределены в пространстве непрерывно, то обе формы уравнений Максвелла — интегральная и дифференциальная - эквивалентны. Однако если имеются поверхности разрыва — поверхности, на которых свойства среды или полей меняются скачкообразно, то интегральная форма уравнений является более общей.
Для того чтобы эти уравнения Максвелла в дифференциальной форме были справедливы и на границах сред, где величины, входящие в уравнения, меняются скачкообразно, необходимо дополнить эти уравнения граничными условиями, которым должно удовлетворять магнитное поле на границе раздела двух сред. Эти соотношения были рассмотрены ранее:

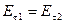 ,
, 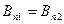 ,
, 
(первое и последнее уравнения выведены для случая, когда на границе раздела нет ни свободных зарядов, ни токов проводимости).
Уравнения Максвелла — наиболее общие уравнения для электрических и магнитных полей в покоящихся средах. Они играют в учении об электромагнетизме такую же роль, как законы Ньютона в механике.
12. Электрический колебательный контур.
Электрическим колебательным контуром называется электрическая цепь состоящая из включенных последовательно катушки индуктивностью L,
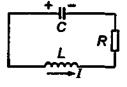 конденсатора емкостью С и резистора сопротивлением R.
конденсатора емкостью С и резистора сопротивлением R.
По закону Ома для участка цепи
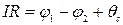 или
или
где q и  , — заряд конденсатора и
, — заряд конденсатора и
разность потенциалов его обкладок в произвольный момент времени t; R — электрическое сопротивление колебательного контура; 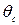 - ЭДС самоиндукции в катушке. Сила тока
- ЭДС самоиндукции в катушке. Сила тока 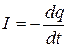 , поэтому дифференциальное уравнение колебаний заряда в колебательном контуре:
, поэтому дифференциальное уравнение колебаний заряда в колебательном контуре:
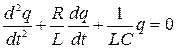
13. Стадии колебаний в идеализированном колебательном контуре.
Идеализированный колебательный контур — колебательный контур, у которого R - 0.
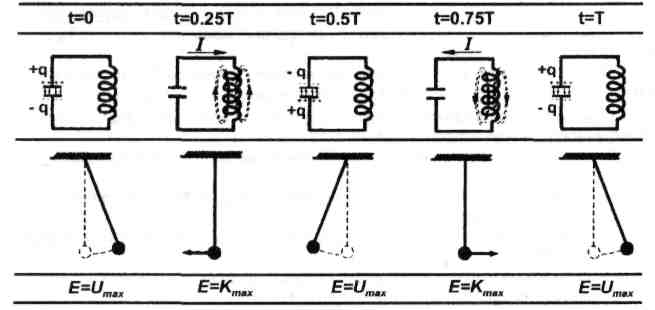
Пусть в начальный момент времени t=0 конденсатор заряжен зарядом q. Тогда энергия электрического поля между обкладками конденсатора 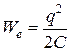 . При замыкании конденсатора на катушку индуктивности, в контуре потечет возрастающий ток I. Энергия электрического поля начнет уменьшаться, а энергия магнитного поля катушки
. При замыкании конденсатора на катушку индуктивности, в контуре потечет возрастающий ток I. Энергия электрического поля начнет уменьшаться, а энергия магнитного поля катушки 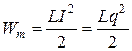 будет
будет
возрастать. Поскольку потерь в контуре нет (R-0), то полная энергия W=We+Wm сохраняется.
В момент времени 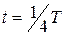 (T-период колебаний), когда конденсатор полностью разрядится, энергия электрического поля обращается в нуль, а энергия магнитного поля (а следовательно, и ток) достигает наибольшего значения.
(T-период колебаний), когда конденсатор полностью разрядится, энергия электрического поля обращается в нуль, а энергия магнитного поля (а следовательно, и ток) достигает наибольшего значения.
Стадии колебаний в контуре можно сопоставить с аналогичными стадиями механических колебаний, например, математического маятника, который в момент времени t = 0 смещен из положения равновесия и имеет максимальную потенциальную энергию E = U max. В момент времени 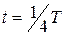 смещение маятника равно нулю, скорость — максимальна, и потенциальная энергия полностью переходит в кинетическую энергию маятника Е = K max.
смещение маятника равно нулю, скорость — максимальна, и потенциальная энергия полностью переходит в кинетическую энергию маятника Е = K max.
Начиная с момента времени 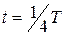 , ток в контуре будет убывать, следовательно, магнитное поле катушки начнет ослабевать. Изменение магнитного поля вызовет индукционный ток, который, по правилу Ленца, будет иметь то же направление, что и ток разрядки конденсатора. Конденсатор начинает перезаряжаться и к моменту времени
, ток в контуре будет убывать, следовательно, магнитное поле катушки начнет ослабевать. Изменение магнитного поля вызовет индукционный ток, который, по правилу Ленца, будет иметь то же направление, что и ток разрядки конденсатора. Конденсатор начинает перезаряжаться и к моменту времени 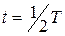 заряд на обкладках конденсатора достигнет максимума, ток в цепи прекратится, и энергия контура снова будет равна энергии электрического поля в конденсаторе.
заряд на обкладках конденсатора достигнет максимума, ток в цепи прекратится, и энергия контура снова будет равна энергии электрического поля в конденсаторе.
Для маятника это будет соответствовать максимальному смещению в направлении, противоположном первоначальному, остановке маятника в крайнем положении (υ =0) и обратному превращению кинетической энергии в потенциальную.
Далее, все процессы в колебательном контуре будут протекать в обратном направлении и система к моменту времени t = Т придет в первоначальное состояние.
Таким образом, в колебательном контуре происходят периодические изменения заряда q на обкладках конденсатора и силы тока I. Эти электрические колебания сопровождаются превращением энергий электрического и магнитного полей.
Из сравнения электрических колебаний с механическими колебаниями, следует, что:
— энергия электрического поля конденсатора аналогична потенциальной энергии маятника,
— энергия магнитного поля катушки аналогична кинетической энергии маятника,
— сила тока в контуре аналогична скорости движения маятника,
— индуктивность L выполняет функцию массы,
— сопротивление R играет роль силы трения, действующей на маятник.
14. Свободные гармонические колебания в колебательном контуре.
Свободные электрические колебания в колебательном контуре являются гармоническими, если его электрическое сопротивление R = 0.
Дифференциальное уравнение свободных гармонических колебаний заряда в контуре:
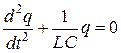
Заряд q совершает гармонические колебания по закону:
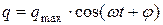
где < 7ти - амплитуда колебаний заряда с циклической частотой:
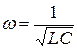
и периодом:
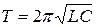 .
.
Эта формула называется — формула Томсона. Сила тока в колебательном контуре:
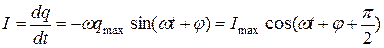 опережает по фазе колебания заряда q на π /2.
опережает по фазе колебания заряда q на π /2.
Здесь 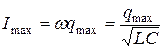 — амплитуда силы тока.
— амплитуда силы тока.
Разность потенциалов обкладок конденсатора 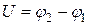 также изменяется по гармоническому закону и совпадает по фазе с зарядом q:
также изменяется по гармоническому закону и совпадает по фазе с зарядом q:
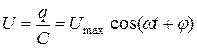
где 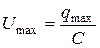 амплитуда разности потенциалов. Амплитуда тока
амплитуда разности потенциалов. Амплитуда тока
 ,
,
Величина 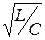 называется волновым сопротивлением колебательного контура.
называется волновым сопротивлением колебательного контура.
26. Примеры свободных затухающих колебаний
Рассмотрим затухающие колебания различной физической природы:
1) механические колебания — пружинный маятник с массой m, который совершает малые колебания под действием упругой силы F = —kх и силы трения 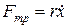 (r —коэффициент сопротивления)
(r —коэффициент сопротивления)
2) электромагнитные колебания — колебания в колебательном контуре состоящем из сопротивления R, индуктивности L и емкости С.
Будем сравнивать оба случая с дифференциальным уравнением cвободных затухающих колебаний линейной системы
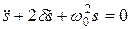
решение которого имеет вид
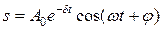
| 1) пружинный маятник | 2) колебательный контур | |
| Колеблющаяся величина | Смещение относительно положения равновесия х | Заряд q |
| Дифференциальное уравнение колебаний | 
| 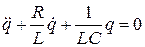
|
| Частота незатухающих колебаний ω 0 | 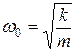
| 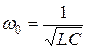
|
| Коэффициент затухания δ | 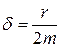
| 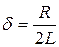
|
Частота незатухающих колебаний 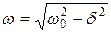
| 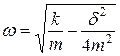
| 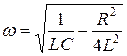
|
| Добротность Q | 
| 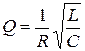
|
| закон колебаний | 
| 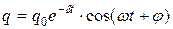
|
27. Вынужденные колебания.
Чтобы в реальной колебательной системе получить незатухающие колебания, надо компенсировать потери энергии. Такая компенсация возможна с помощью какого-либо периодически действующего фактора X(t), изменяющегося по гармоническому закону:
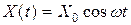
В случае механических колебаний таким фактором является вынуждающая cuлa 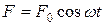 . Закон движения для пружинного маятника будет иметь вид
. Закон движения для пружинного маятника будет иметь вид
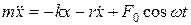
В случае электрического колебательного контура роль X(t) играет подводимая к контуру внешняя ЭДС или переменное напряжение U = Um cosω t. Уравнение колебаний в контуре будет иметь вид
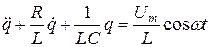
В общем виде дифференциальное уравнение вынужденных колебаний имеет вид
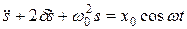
Это уравнение — линейное неоднородное дифференциальное уравнение. Его р ешение равно сумме общего решения 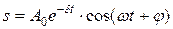 однородного уравнения и частного решения неоднородного уравнения. Можно показать, частное решение имеет вид
однородного уравнения и частного решения неоднородного уравнения. Можно показать, частное решение имеет вид
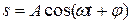
где А и ω задаются формулами
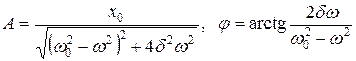
Так для электромагнитных колебаний, если обозначить a — сдвиг по фазе между зарядом и приложенным напряжением, то можно показать, что решение дифференциального уравнения будет иметь вид  ,
,
где
