
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Электромагнитные волны. 47. Электромагнитные волны.
|
|
47. Электромагнитные волны.
Электромагнитные волны — это переменное электромагнитное поле, распространяющееся в пространстве с конечной скоростью.
Существование электромагнитных волн вытекает из уравнений Максвелла: 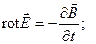
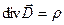 ;
;  ;
;  ,
,
которые в области пространства, не содержащей свободных электрических зарядов и макроскопических токов, имеют вид
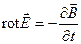 ;
; 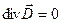 ;
; 
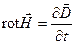 ;
; 
Если среда — однородный и изотропный диэлектрик, не обладающий сегнетоэлектрическими или ферромагнитными свойствами, то 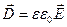 и
и  , где
, где 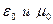 — электрическая и магнитная постоянные, ε и μ — диэлектрическая и магнитная проницаемости среды.
— электрическая и магнитная постоянные, ε и μ — диэлектрическая и магнитная проницаемости среды.
В этом случае уравнения Максвелла
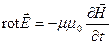 ;
; 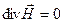 ;
;  ;
; 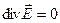
Используя 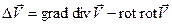 получим волновые уравнения для векторов
получим волновые уравнения для векторов 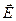 и
и 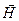 :
:
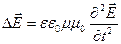 ,
, 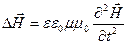
где 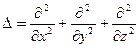 — оператор Лапласа,
— оператор Лапласа, 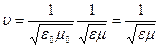 - фазовая скорость электромагнитной волны,
- фазовая скорость электромагнитной волны, 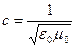 — скорость света ввакууме. Таким образом, электромагнитные поля действительно могут существовать в виде электромагнитных волн.
— скорость света ввакууме. Таким образом, электромагнитные поля действительно могут существовать в виде электромагнитных волн.
Поскольку 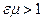 , то
, то 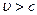 — скорость распространения электромагнитных волн в веществе всегда меньше, чем в вакууме.
— скорость распространения электромагнитных волн в веществе всегда меньше, чем в вакууме.
48. Поперечность электромагнитных волн.
Следствия теории Максвелла:
(1) Векторы £ и Я напряженностей электрического и магнитного полей волны взаимно перпендикулярны и лежат в плоскости, перпендикулярной вектору 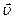 скорости распространения волны, причем векторы
скорости распространения волны, причем векторы 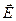 ,
, 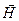 и
и 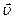 образуют правовинтовую систему. (Только
образуют правовинтовую систему. (Только 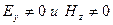 )
)

(2) В электромагнитной волне векторы 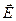 и
и 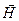 всегда колеблются в одинаковых фазах, причем мгновенные значения E и H в любой точке связаны соотношением
всегда колеблются в одинаковых фазах, причем мгновенные значения E и H в любой точке связаны соотношением 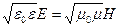
Волновым уравнениям: 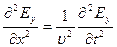 ,
, 

удовлетворяют плоские монохроматические электромагнитные волны, описываемые уравнениями 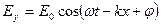 ,
, 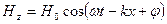 ,
,
где Е0 и Н0 — амплитуды напряженностей электрического и магнитного полей
волны, ω — круговая частота волны, 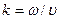 — волновое число, φ —
— волновое число, φ —
начальная фаза колебаний (одинаковая, поскольку колебания 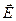 и
и 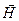 происходят с одинаковой фазой).
происходят с одинаковой фазой).
49. Отражение и преломление электромагнитных волн на границе раздела двух диэлектрических сред.
Пусть на границу раздела двух диэлектриков падает плоская электромагнитная волна. В таком случае, как показывает опыт, от границы раздела диэлектриков будут распространяться две плоские волны — отраженная и преломленная.
Запишем выражения для падающей (i), отраженной (r) и преломленной (d) волн в комплексной экспоненциальной форме:
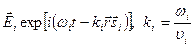 ;
;
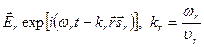 ;
;
 .
.
Здесь  — радиус-вектор, ω и υ — частота и скорости волн,
— радиус-вектор, ω и υ — частота и скорости волн, 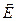 — амплитуды волн,
— амплитуды волн, 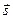 — единичные векторы, показывающие направление распространения соответствующих волн. Условие
— единичные векторы, показывающие направление распространения соответствующих волн. Условие 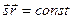 определяет плоскость, перпендикулярную к
определяет плоскость, перпендикулярную к 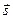 , поэтому данная система выражений описывает плоские волны, распространяющиеся вдоль векторов
, поэтому данная система выражений описывает плоские волны, распространяющиеся вдоль векторов 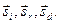
Граничные условия для тангенциальных (τ) компонент векторов напряженности электрического и магнитного поля в любой точке границы раздела сред (1) и (2) имеют вид (см. 4-п.45): 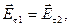
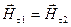
Для нашего случая, граничные условия для электрического вектора:
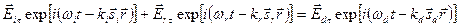
Для выполнения этого равенства в любой момент времени t в любой точке границы раздела необходимо и достаточно, чтобы во всех трех показателях экспонент были одинаковы коэффициенты при t и при проекции  радиус-вектора
радиус-вектора  на границу раздела, т.е. чтобы выполнялись равенства:
на границу раздела, т.е. чтобы выполнялись равенства:
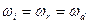 ;
;
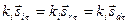 .
.
Следовательно, частоты всех трех волн должны быть равны междусобой, поскольку частоты колебаний зарядов в диэлектрической среде, вынуждаемых колебаниями электрического вектора, совпадают с частотой вынуждающей силы. Кроме того, единичные векторы 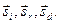 находятся в одной плоскости, проходящей через нормаль к плоскости раздела (плоскость падения).
находятся в одной плоскости, проходящей через нормаль к плоскости раздела (плоскость падения).
Выберем систему координат таким образом, чтобы плоскость хОу совпадала с плоскостью раздела сред, а плоскость zОх — с плоскостью падения, причем ось Оz направим из среды I в среду II (см. рисунок).
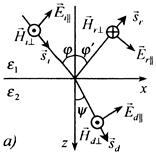

Обозначим φ — угол между  , и осью Оz (угол падения) π —
, и осью Оz (угол падения) π — 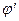 угол между
угол между 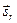 и Оz: (
и Оz: (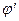 —угол отражения), ψ — угол между
—угол отражения), ψ — угол между 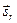 и Оz (угол преломления). В этой системе координат у-компоненты векторов
и Оz (угол преломления). В этой системе координат у-компоненты векторов 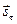 равны нулю, а х-компоненты можно выразить следующим образом:
равны нулю, а х-компоненты можно выразить следующим образом:

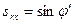 ,
, 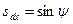
Следовательно, равенство 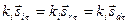 примет вид:
примет вид:
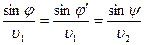

Первое равенство означает, что 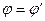 — закон отражения в оптике.
— закон отражения в оптике.
Из второго равенства следует оптический закон преломления.
Показателем преломления среды п называется величина, равная отношению скорости с электромагнитных волн в вакууме к их фазовой скорости υ в среде:
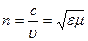
Для среды, не обладающей ферромагнитными свойствами,  и практически можно считать, что
и практически можно считать, что
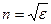
 В этом случае для преломленной волны имеем закон преломления:
В этом случае для преломленной волны имеем закон преломления:
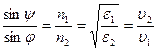
Разложим амплитуды электрического и магнитного векторов на компоненты  , лежащие соответственно в плоскости падения и перпендикулярные к ней. Взаимные ориентации векторов
, лежащие соответственно в плоскости падения и перпендикулярные к ней. Взаимные ориентации векторов 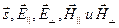 приведены на рисунках (а) и (б).
приведены на рисунках (а) и (б).
Для компонент напряженности электрического вектора, лежащих в плоскости падения (рис. (а)), граничные условия (с учетом 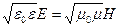 ,
,  ) имеют вид:
) имеют вид:
 и
и 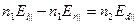
Решая эту систему уравнений и используя закон преломления, найдем выражения для амплитудных коэффициентов отражения 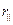 и пропускания
и пропускания 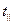 , для волны, линейно-поляризованной в плоскости падения:
, для волны, линейно-поляризованной в плоскости падения:
 (*)
(*)
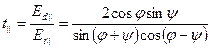
Для компонент напряженностей электрического вектора, перпендикулярных к плоскости падения (рис. (б)), граничные условия принимают вид:
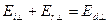 и
и 
Амплитудные коэффициенты отражения и пропускания  и
и  :
:
 (**)
(**)
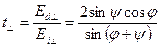
Соотношения (*) и (**) между амплитудами падающей, отраженной и преломленной волн называются формулами Френеля.
В формулах Френеля 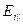 , и
, и  — величины положительные, а
— величины положительные, а 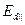 и
и 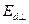 при любых возможных углах падения и преломления также положительны, что свидетельствует о совпадении фаз преломленной и падающей волн. Величины
при любых возможных углах падения и преломления также положительны, что свидетельствует о совпадении фаз преломленной и падающей волн. Величины  , и
, и 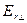 могут быть как отрицательными, так и положительными. В первом случае фаза колебаний вектора
могут быть как отрицательными, так и положительными. В первом случае фаза колебаний вектора 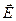 изменяется при отражении на π (фаза колебаний вектора
изменяется при отражении на π (фаза колебаний вектора 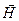 при этом сохраняется). Во втором случае (см. рис.) отражение происходит без изменения фазы колебаний вектора
при этом сохраняется). Во втором случае (см. рис.) отражение происходит без изменения фазы колебаний вектора 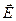 (соответственно фаза колебаний вектора
(соответственно фаза колебаний вектора 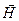 при отражении изменяется на π). Значения сдвига фаз колебаний вектора
при отражении изменяется на π). Значения сдвига фаз колебаний вектора 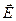 при отражении электромагнитных волн в зависимости от угла падения и значений показателей приведены в таблице.
при отражении электромагнитных волн в зависимости от угла падения и значений показателей приведены в таблице.
| Сдвиг фаз между компонентами | 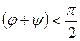
| 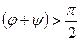
| ||
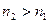 или или 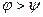
|  или или 
| 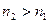 или или 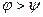
|  или или 
| |
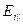 и и 
| π | π | ||
 и и 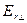
| π | π |
Таким образом, при малых углах падения 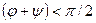 фаза обеих компонент электрического вектора отраженной волны противоположна фазе падающей для случая, когда
фаза обеих компонент электрического вектора отраженной волны противоположна фазе падающей для случая, когда 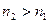 , и совпадает с фазой падающей волны при
, и совпадает с фазой падающей волны при  . В частности это имеет место и при нормальном падении.
. В частности это имеет место и при нормальном падении.
Явление изменения фазы волны на π при отражении от среды с большим показателем преломления — " потеря полуволны" — играет значительную роль в интерференционных и дифракционных явлениях, которые рассматриваются в курсе " Оптика".
Рассмотрим теперь случай, когда выполняется условие  (и, следовательно,
(и, следовательно, 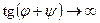 ). Угол падения φ, при котором отраженный и преломленный лучи взаимно перпендикулярны, называется углом Брюстера.
). Угол падения φ, при котором отраженный и преломленный лучи взаимно перпендикулярны, называется углом Брюстера.
Из закона преломления следует, что  .
.
При этом 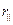 и в отраженной волне присутствует только
и в отраженной волне присутствует только 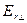 компонента (отраженная волна линейно поляризована в плоскости, перпендикулярной плоскости падения).
компонента (отраженная волна линейно поляризована в плоскости, перпендикулярной плоскости падения).
50. Энергия электромагнитных волн.
Объемная плотность w энергии электромагнитной волны складывается из объемных плотностей 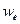 и wm электрического и магнитного полей:
и wm электрического и магнитного полей:
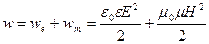 .
.
Плотность потока энергии  .
.