
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Функция потерь качества по Тагути
|
|
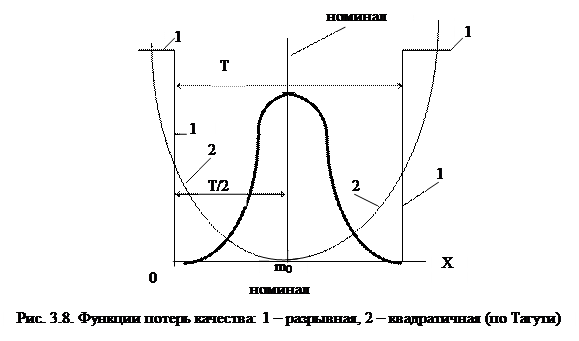
Японский ученый Г. Тагути предложил новый подход к оценке качества изготовления продукции. Традиционное представление о качестве продукции заключается в том, что все изготовленные изделия являются в равной степени качественными, если их показатели (или параметры) качества соответствуют требованиям технической документации, в которой определен допуск на эти показатели (параметры). Другими словами, внутри зоны допуска потери качества равны нулю. Если же показатели качества выходят за границы допуска, то потери качества объявляются неприемлемыми. Такую функцию потерь качества (рис. 3.8) Тагути назвал «разрывной порогообразной функцией» [28, 41, 42].
В свою очередь Г. Тагути предложил функцию потерь качества L(Х), по которой качественными считаются только такие показатели, значения которых полностью совпадают по величине с номинальными значениями этих показателей, а всякое отклонение от номинала сопряжено с той или иной потерей качества продукции (рис. 3.8):
L(Х) = k (Х – mо)², (3.1)
где mо – номинальное значение показателя (параметра) качества,
k – постоянный коэффициент, характеризующий денежный эквивалент,
Х – текущее значение показателя (параметра) качества.
 |
При этом потери качества растут в квадратичной зависимости по мере отклонения истинных (измеренных) значений параметра от номинального и могут иметь место, как у изготовителя, так и у потребителя (заказчика) продукции. Сам Г. Тагути квадратичную зависимость объяснил следующим образом: «Если постепенные отклонения от номинала дают непропорциональное увеличение потерь, то, скорее всего, это квадратичные увеличения».
Вернемся к уравнению (3.1). Если известна величина потерь на границах допуска Т, то легко рассчитать значения постоянного коэффициента k. Если допустить, что допуск на параметр качества симметричен относительно номинала mо, а величина потерь на любой из границ допуска одинакова и равна Lо, то имеем
4 Lо
k = ——.
Т²
Формула (3.1) соответствует экономическим потерям качества единичного измерения показателя качества в зависимости от его расположения в поле рассеяния относительно координаты номинального значения параметра mо. В случае массового (или серийного) изготовления деталей, когда отбраковка производится не по величине показателя, а по калибру (проходной, непроходной), можно судить о качестве только среднестатистической детали (вернее ее показателя качества). Для этого необходимо предварительно вычислить суммарные потери качества всей совокупности деталей (или величин показателей качества).
Допустим, что случайный показатель качества Х распределен с плотностью вероятности f(X).
Суммарные потери качества распределения SΣ случайных значений Х можно определить по уравнению
T
SΣ = ∫ f(X)∙ L(X)dX, (3.3)
o
где Т – допуск на размер показателя качества Х.
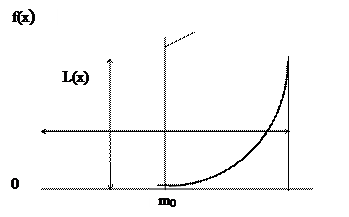
Учитывая сложность аналитического решения выражения (3.3), воспользуемся наиболее простым (математически) законом равномерного распределения, где плотность вероятности является постоянной величиной f(X) = a (рис. 3.9):
 | |||
 | |||
|
 | |||
|
Подставим L(X) и f(X) в уравнение (3.3). При симметричном расположении поля допуска относительно номинального размера mо имеем:
T
SΣ = ∫ a∙ k∙ (X – T/2)² dx = akT³ /12.
Учитывая, что общее число случайных значений параметра n в поле равномерного распределения равно aT, окончательно получим
SΣ = 0, 082 nkT². (3.4)
Наибольший интерес для практики представляет нормальное распределение случайной величины Х. К сожалению, в этом случае (при математически сложном выражении для плотности вероятности) уравнение (3.3) не имеет аналитического решения. Решение же в численном виде с применением компьютера не даст «пищи» для анализа закономерностей. Поэтому воспользуемся приближенным вычислением суммарных потерь качества Sо через алгебраическую сумму потерь качества в каждом интервале поля рассеяния ω, равным одной сигме σ:
r
Sо = Σ L(Δ i)∙ n∙ qi, (3.5)
где L(Δ i) – величина функции потерь качества для координаты середины i – го интервала,
Δ i – координата середины i- го интервала,
qi – вероятность попадания случайной величины Х в i- й интервал,
n – общее число случайных значений параметра,
r – число интервалов.
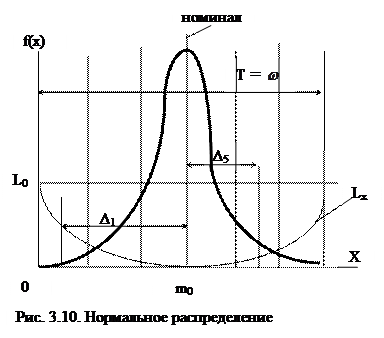
Для простоты вычислений принимаем, что поле рассеяния равно полю допуска (6σ = Т), а координата середины поля рассеяния m совпадает с серединой поля допуска (рис.3.10). Одновременно допуск симметричен относительно номинального размера показателя качества mо, то есть m =mо. Для каждого интервала, равного одному среднеквадратическому отклонению σ, вычислим долю измерений, попавших в данный интервал, и значение функции потерь, соответствующее середине данного интервала. Размерные параметры L(Δ) выразим через величину допуска Т и коэффициент к (кТ²), а долю размеров в каждом интервале через долю от общего числа измерений n. Так, например, для первого интервала, равного Т/6, координата середины интервала равна Т/12. Тогда L(Δ 1) = к (Т/12 – 6Т/12)² = 0, 17кТ². Доля размеров в первом интервале равна 0, 02 n.
Занесем вычисления L(Δ) и q для каждого из шести интервалов в табл. 3.6. По результатам вычислений отметим, что суммарные потери качества значений показателей качества Х при нормальном законе распределения (при условии равенства поля допуска Т полю рассеяния 6σ и симметричном поле допуска относительно номинального размера) составляют
Sо =0, 029nkT². (3.6)
 |
Сравнивая значения суммарных потерь по формулам (3.4) и (3.6), можно отметить, что потери качества при распределении случайной величины по закону Гаусса в 2, 8 меньше, чем потери качества при распределении по закону равномерной плотности вероятности
Таблица 3.6
| m = mо | 1σ | 2σ | 3σ | 4σ | 5σ | 6σ | Сумма |
| L(Δ), кТ² | 0, 17 | 0, 062 | 0, 007 | 0, 007 | 0, 062 | 0, 17 | |
| q, n | 0, 02 | 0, 14 | 0, 34 | 0, 34 | 0, 14 | 0, 02 | |
| L(Δ)∙ q | 0, 0034 | 0, 0087 | 0, 0024 | 0, 0024 | 0, 0087 | 0, 0034 | 0, 029 |
Подставляя в формулу (3.6) значения кТ² из формулы (3.2), получим суммарную величину потерь в денежном выражении:
Sо = 0, 116 n Lо.
Для среднестатистического показателя качества удельные потери качества Sσ составят
Sσ = Sо/n = 0, 029 кТ² = 0, 116 Lо. (3.7)
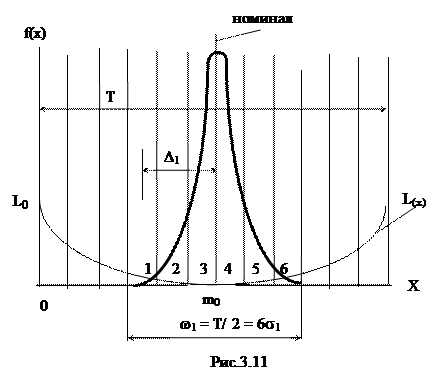
Рассмотрим случай, когда поле рассеяния ω 1 значительно меньше (в 2 раза), чем поле допуска, но координата середины поля рассеяния и середины поля допуска совпадают. Этот случай имеет место, когда технологическая система обеспечивает такое рассеяние измеренных показателей качества, которое соответствует методу «Шесть сигм» (рис.3.11). Очевидно, что при этом σ 1 = σ /2, где σ – среднеквадратическое отклонение для случая ω = Т.
 |
Для оценки потерь качества при изготовлении деталей по методу «Шесть сигм» проведем вычисление суммарных потерь по уравнению (3.5). Разделим поле допуска на 12 интервалов, чтобы каждый интервал соответствовал σ 1. Очевидно, что доля измерений в каждом интервале σ 1 в поле ω 1 будет такой же, как в каждом интервале σ поля рассеяния ω.
Для примера, вычислим для первого интервала σ 1 функцию потерь качества:
L(Δ) = к (7Т/24 – 12Т/24)² = 0, 043кТ².
Занесем расчетные данные по каждому интервалу в табл. 3.7.
Анализируя результаты расчета в табл. 3.7, отметим, как и следовало ожидать, что потери качества среднестатистического показателя, полученные по методу «Шесть сигм», Sσ 1 = 0, 0073 кТ² = 0, 0292 Lо значительно (в 4 раза) меньше, чем в случае ω = Т.
Таблица 3.7
| m = mо | 1σ 1 | 2σ 1 | 3σ 1 | 4σ 1 | 5σ 1 | 6σ 1 | Сумма |
| L(Δ), кТ² | 0, 043 | 0, 0156 | 0, 0017 | 0, 0017 | 0, 0156 | 0, 043 | |
| q, n | 0, 02 | 0, 14 | 0, 34 | 0, 34 | 0, 14 | 0, 02 | |
| L(Δ)∙ q | 0, 00086 | 0, 0022 | 0, 00058 | 0, 00058 | 0, 0022 | 0, 00086 | 0, 0073 |
Из данных таблиц 3.6 и 3.7 можно вывести следующую зависимость:
Sσ 1 / Sσ 2 = (σ 1 / σ 2)²,
то есть суммарные потери качества нормального распределения со среднеквадратическим отклонением параметра σ 1 относятся к суммарным потерям качества нормального распределения со среднеквадратическим отклонением параметра σ 2 как квадрат отношения их среднеквадратических отклонений (при условии, что у них одинаковый допуск и координаты середин поля рассеяния и поля допуска совпадают с номинальным размером параметра).
До сих пор нами рассматривалась идеальная схема распределения случайных величин, при которой координата середины поля рассеяния совпадает с серединой поля допуска.
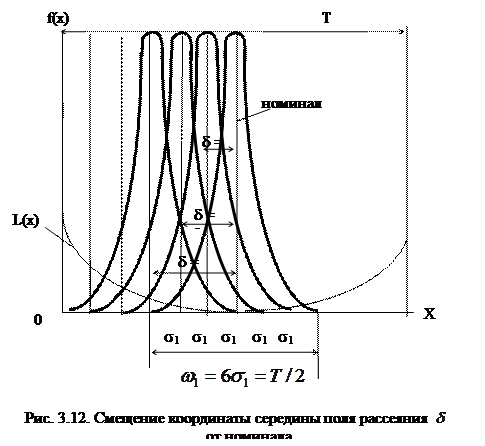
Рассмотрим, как изменяется суммарные потери качества при смещении δ координаты середины поля рассеяния от середины поля допуска на величину равную 1σ 1, 2σ 1 и 3σ 1 соответственно (рис. 3.12). При этом 6σ 1 = Т/2.
Занесем в табл. 3.8 данные вычислений по формуле (3.5).
Таблица 3.8
| Σ 1 | 1σ 1 | 2σ 1 | 3σ 1 | 4σ 1 | 5σ 1 | 6σ 1 | Сумма |
| δ = 0 | |||||||
| L(Δ) | 0, 043 | 0, 0156 | 0, 0017 | 0, 0017 | 0, 0156 | 0, 043 | |
| Q | 0, 02 | 0, 14 | 0, 34 | 0, 34 | 0, 14 | 0, 02 | |
| L(Δ)∙ q | 0, 00086 | 0, 0022 | 0, 00058 | 0, 00058 | 0, 0022 | 0, 00086 | 0, 0073 |
| δ = 1σ 1 | |||||||
| L(Δ) | 0, 085 | 0, 043 | 0, 0156 | 0, 0017 | 0, 0017 | 0, 0156 | |
| Q | 0, 02 | 0, 14 | 0, 34 | 0, 34 | 0, 14 | 0, 02 | |
| L(Δ)∙ q | 0, 0017 | 0, 006 | 0, 0053 | 0, 0006 | 0, 00024 | 0, 0003 | 0, 014 |
| δ = 2σ 1 | |||||||
| L(Δ) | 0, 14 | 0, 085 | 0, 043 | 0, 0156 | 0, 0017 | 0, 0017 | |
| Q | 0, 02 | 0, 14 | 0, 34 | 0, 34 | 0, 14 | 0, 02 | |
| L(Δ) ∙ q | 0, 0028 | 0, 0119 | 0, 0146 | 0, 0053 | 0, 00024 | 0, 00003 | 0, 035 |
| δ =3σ 1 | |||||||
| L(Δ) | 0, 21 | 0, 14 | 0, 085 | 0, 043 | 0, 0156 | 0, 0017 | |
| Q | 0, 02 | 0, 14 | 0, 34 | 0, 34 | 0, 14 | 0, 02 | |
| L(Δ) ∙ q | 0, 0042 | 0, 0196 | 0, 029 | 0, 0146 | 0, 0002 | 0, 0003 | 0, 069 |
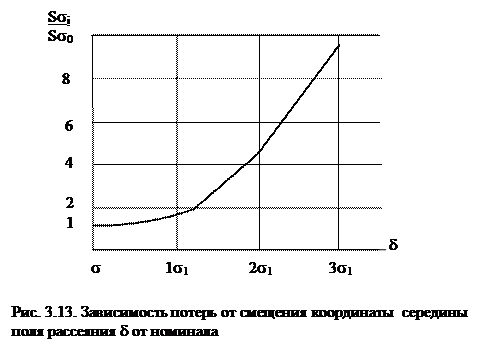
Данные табл. 3.8 показывают, что с увеличением смещения δ потери качества растут почти в геометрической прогрессии (рис. 3.13).
Следует отметить, что потери качества при смещении на 2σ 1 уже выше, чем суммарные потери в случае отсутствия смещения при ω = Т. Таким образом, смещение поля рассеяния δ оказывает более сильное влияние на потери качества, чем увеличение самого поля рассеяния ω, расположенного симметрично относительно номинала.
Рассмотренные выше варианты потерь качества имели отношение к случаям симметричного расположения допуска относительно номинального значения параметра. На практике не меньшее распространение имеют случаи, когда номинальный размер параметра располагается на границе поля допуска, т.е. допуск – не симметричный (рис. 3.14). Такое расположение номинальных значений параметра особенно часто встречается в трехзвенных размерных цепях, когда необходимо обеспечить соединение деталей или их вращение относительно друг друга.
 | |||
 |
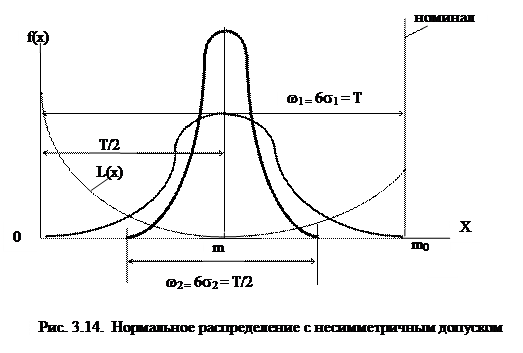 |
Рассчитаем суммарные потери качества по формуле (3.5) при несимметричном допуске для случаев ω 1 = Т и ω 2 = Т/2. В обоих случаях координата середины поля рассеяния совпадает с серединой поля допуска.
Результаты расчета сведем в табл. 3.9.
Таблица 3.9
| m ≠ mо | 1σ | 2σ | 3σ | 4σ | 5σ | 6σ | Сумма |
| σ 1 | |||||||
| L(Δ) | 0, 84 | 0, 56 | 0, 34 | 0, 174 | 0, 062 | 0, 007 | |
| q | 0, 02 | 0, 14 | 0, 34 | 0, 34 | 0, 14 | 0, 02 | |
| L(Δ)∙ q | 0, 0168 | 0, 0784 | 0, 1156 | 0, 0592 | 0, 0087 | 0, 00014 | 0, 28 |
| σ 2 | |||||||
| L(Δ) | 0, 50 | 0, 39 | 0, 29 | 0, 21 | 0, 14 | 0, 085 | |
| q | 0, 02 | 0, 14 | 0, 34 | 0, 34 | 0, 14 | 0, 02 | |
| L(Δ)∙ q | 0, 010 | 0, 055 | 0, 098 | 0, 071 | 0, 020 | 0, 002 | 0, 068 |
Потери качества при несимметричном допуске, как и ожидалось, оказались выше у показателей качества с большим полем рассеяния ω:
Sσ 1 = 0, 28 кТ² = 1, 12 Lо; Sσ 2 = 0, 068 кТ² = 0, 272 Lо.
Если сравнивать потери качества при разных вариантах расположения номинального значения параметра (в середине поля допуска или на его границе), то видим, что потери качества среднестатистического параметра качества при несимметричном варианте выше почти в 10 раз:
Sσ 1 (m ≠ mo) 0, 28кТ²

 = = 9, 5.
= = 9, 5.
Sσ (m = m0) 0, 029кТ²
Аналогичное соотношение имеет место и для Sσ 2.
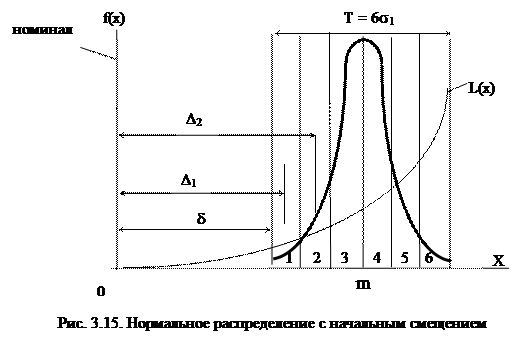
Рассмотрим еще один вариант положения номинального размера параметра относительно левой границы допуска Т со смещением δ (рис. 3.15).При этом поле рассеяния равно полю допуска.
Вычислим функцию потерь качества для первого интервала поля рассеяния по формуле (3.1):
L(Δ 1) = к (δ + Т/12)². (3.8)
Чтобы упростить расчеты, выразим величину смещения через часть поля допуска: δ = sТ. Тогда формула (3.8) для i – го интервала будет иметь вид:
2i - 1
L(Δ i) = кТ² (s + ——)². (3.9)
 |
Сведем в табл. 3.10 результаты расчета потерь качества распределения по формуле (3.9) при s =1.
Таблица 3.10
| s = 1 | 1σ | 2σ | 3σ | 4σ | 5σ | 6σ | Cумма |
| L(Δ), кТ² | 1, 17 | 1, 56 | 2, 01 | 2, 51 | 3, 06 | 3, 67 | |
| q, n | 0, 02 | 0, 14 | 0, 34 | 0, 34 | 0, 14 | 0, 02 | |
| L(Δ) · q | 0, 023 | 0, 218 | 0, 68 | 0, 85 | 0, 43 | 0, 07 | 2, 27 |
Суммарные потери такого варианта расположения номинального размера и поля рассеяния исключительно велики и составляют
Sо = 2, 27 n кТ².
Отметим, что среднестатистические потери качества распределения в первых трех интервалах (левой половине) поля рассеяния составляют 0, 96 кТ², что в 2, 5 раза ниже, чем среднестатистические потери по всему распределению.
Все предшествующие расчеты и размышления имели отношение к одной детали или к разбросу параметра качества при изготовлении детали. На практике изолировано друг от друга детали не применяются, и рассуждения о влиянии положении номинального размера при обеспечении взаимозаменяемости деталей на величину потерь качества следует перенести на их сборочное соединение. Необходимо оценить положение номинального размера параметра относительно допуска замыкающего (или исходного) звена размерной цепи. В данном случае – это конструкторская размерная цепь. Но потери качества не абстрактны, а конкретны, и зависят не столько от самого допуска, сколько от расположения распределения случайной величины (параметра) в поле допуска.
Допустим, что имеется плоская размерная цепь из пяти звеньев. В них четыре составляющих звена: А1 = 35 +0.16, А2 = 60 – 0, 30, А3 = 20 +0, 1, А4 = 40+0, 18. Определим величину номинального размера замыкающего звена А0 и величину его верхнего и нижнего предельных отклонений ЕSA и ISA по методу полной взаимозаменяемости, если звенья А2 и А3 – увеличивающие, а звенья А1 и А4 – уменьшающие. Тогда Ао = А2 + А3 – А1 – А4 = 5 мм.
Из теории размерных цепей [67] известно, что верхнее ES и нижнее EI предельные отклонения номинального размера замыкающего звена определяются по следующим формулам:
ESA0 = (ESA2 + ESA3) – (EIA1 + EIA4) = (0 +0, 13) – (0+0) = 0, 13 мм
EIA0 = (EIA2 + EIA3) – (ESA1 + ESA4) =
= (-0, 30 + 0) – (0, 16 +0, 18) = - 0, 64 мм
Таким образом, допуск замыкающего звена равен 0, 77 мм, а положение номинального размера в поле допуска выглядит в виде 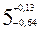 .
.
Допустим также, что распределение параметра А0 подчиняется нормальному закону (рис. 3.16), и поле рассеяния 6σ равно полю допуска Т= 0, 77 мм (σ = 0, 13 мм). Если известны потери качества на границах поля допуска и величина смещения середины поля рассеяния относительно номинала (в нашем случае 0, 26 мм, что составляет примерно 2σ), не представляет сложности по формуле (3.5) рассчитать суммарные потери качества распределения.
Сведем в таблицу 3.11 результаты расчета составляющих потерь качества L(Δ) и q.
Таблица 3.11
| m ≠ m0 | 1σ | 2σ | 3σ | 4σ | 5σ | 6σ | Сумма |
| L(Δ) | 0, 56 | 0, 34 | 0, 174 | 0, 062 | 0, 007 | 0, 007 | |
| Q | 0, 02 | 0, 14 | 0, 34 | 0, 34 | 0, 14 | 0, 02 | |
| L(Δ) • q | 0, 011 | 0, 048 | 0, 059 | 0, 021 | 0, 001 | 0, 00014 | 0, 130 |

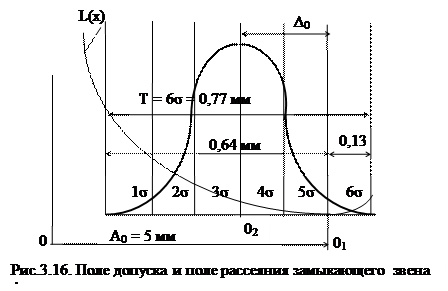
На основании данных табл. 3.11 определим суммарные потери качества распределения замыкающего звена А0:
S0 = 0, 13 ◦ n ◦ k ◦ T2 = 0, 52 ◦ nL0, (3.10)
где n – число случайных значений параметра А0 в поле рассеяния.
Для среднестатистического значения показателя качества удельные потери составят
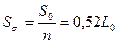 ,
,
где L0 – стоимость потерь качества на границе допуска.
Если использовать для расчета допуска замыкающего звена метод неполной взаимозаменяемости, то поле допуска Ао уменьшится до 0, 41 мм, из которых 0, 07 мм – верхнее предельное отклонение, а 0, 34 мм – нижнее предельное отклонение. Среднеквадратическое отклонение σ 1 = 0, 07 мм.
Сравним потери качества распределения А0, полученные при определении допуска замыкающего звена по методу полной взаимозаменяемости (МПВ), с потерями качества распределения при определении допуска замыкающего звена по методу неполной взаимозаменяемости (МНПВ).
Учитывая, что соотношение верхнего и нижнего предельных отклонений допуска от номинала для распределений с σ и σ 1 совпадают:
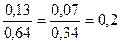 ,
,
а также совпадают смещения Δ 0 (равные двум сигма) середины поля рассеяния от номинала, можно в расчете потерь качества распределения с σ 1 использовать формулу (3.10), но, естественно, со своими значением допуска Т1 и стоимостью потерь на границе допуска L01:
S01 = 0, 13 • n • kT1² = 0, 51 • nL01.
Отсюда легко показать, что суммарные потери качества распределения (при n = const) при расчете допуска по МПВ будут относиться к величине суммарных потерь качества распределения при расчете допуска по МНПВ как квадрат отношения величин их допусков
 .
.
То есть, если определение допусков замыкающего звена размерной цепи ведется по методу НПВ, исходя из нормального закона распределения, то соотношение α = 3 сохраняется для любых значений допусков.
При многозвенных размерных цепях, в которых допуск замыкающего звена рассчитывается с применением метода неполной взаимозаменяемости, а номинальное значение параметра лежит, как правило, в пределах поля допуска и значительно реже – на его границе, потери качества сборочного соединения относительно невелики.
Более высокие потери качества имеют место в трехзвенных размерных цепях, в которых номинал часто располагается на границах допуска. В качестве примера малозвенной (трехзвенной) размерной цепи выбираем пару скольжения (вал – втулка).
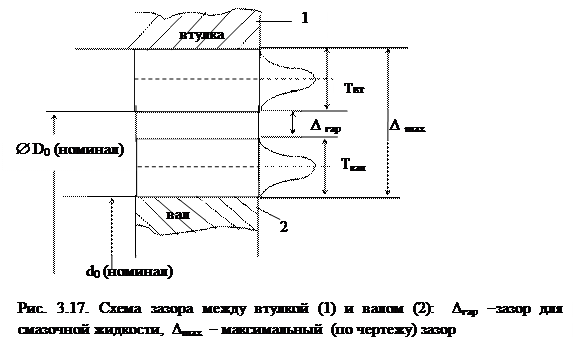
Сегодняшняя практика обеспечения качества функционирования пары скольжения связана с высокой точностью механической обработки поверхностей скольжения. Если рассматривать пару вал - втулка как размерную цепь, то замыкающим звеном будет зазор в соединении, величина которого зависит от величин допусков вала и втулки и величины гарантированного зазора, обеспечивающего отсутствие металлического контакта сопрягаемых деталей (рис. 3.17). Как правило, в этом гарантированном зазоре циркулирует смазочная жидкость. Учитывая минимальное количество звеньев размерной цепи (три), величина допуска на замыкающее звено определяется по методу полной взаимозаменяемости, то есть арифметическим сложением допусков составляющих звеньев (вал, втулка) и гарантированного зазора:
∆ max = Твал + Твт + ∆ гар, (3.11)
где Твал, Твт – соответственно допуски на диаметр вала и диаметр втулки,
∆ гар – гарантированный зазор.
Допустим, что поле рассеяния размеров диаметров при изготовлении вала и втулки будут равны полям соответствующих допусков. Очевидно, что величины функции потерь качества, как для вала, так и для втулки, будут предельно велики, так как имеет место максимальное смещение между номинальным значением соединения Dо и координатами середины поля рассеяния вала и втулки (при условии, что поле рассеяния примерно равно полю допуска). Суммарные потери качества среднестатистической сборки пары скольжения будут определяться суммой потерь среднестатистических составляющих этой сборки. Если принять, что гарантированный зазор Δ гар = 0, то суммарные среднестатистические потери качества соединения можно определить по формуле (3.12):
Sсбор = Sвал + Sвт = 0, 28 к (Т² вал + Т² вт). (3.12)
 |
В случае наличия гарантированного зазора суммарные среднестатистические потери соединения необходимо определять по результатам расчетов, приведенных в таблицах 3.9 и 3.10. Если принять s=1 (что весьма близко к стандартам допусков при посадке с зазором), то
Sсбор = 0, 28 кТ² вт + 2, 27 кТ² вал. (3.13)
Если судить по предыдущим расчетам потерь качества в настоящей работе, то суммарные потери среднестатистической сборки нужно считать значительными, что не позволит (по Тагути) обеспечить надежного сопряжения.
Как улучшить качество пары скольжения? Каким образом снизить суммарные потери качества?
Анализируя потери качества, мы уже обращали внимание на значительную разницу суммарных потерь качества в ближней и дальней (от положения номинального значения параметра) половине поля рассеяния (или поля допуска).
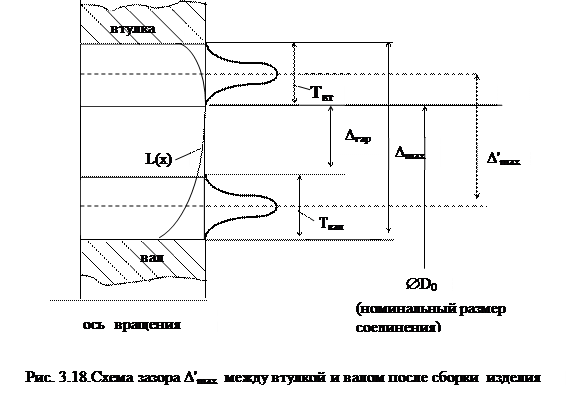
Если качество пары скольжения имеет приоритетное значение для безотказной работы всего узла, то из экономических соображений есть смысл провести сортировку размеров диаметров вала и втулки, соответствующих непроходному калибру по середине поля допуска. Тогда максимальное значение зазора ∆ ′ max между валом и втулкой при сборке (рис. 3.18) будет равно:
Δ ′ max = 0, 5 (Твал + Твт) + Δ гар. (3.14)
Суммарные же потери качества среднестатистической пары скольжения составят (при условии равенства допусков вала и втулки и s= 1) 1, 036 кТ², что в 2, 5 раза меньше, чем по формуле (3.13).
При этом, по сравнению со стандартной сборкой, обеспечивается не только величина зазора, близкого к оптимальному, но и значительно снижаются потери качества сборки пары скольжения.
Отсортированные детали (по другую сторону половины допуска) не уходят в брак, потому что полностью соответствуют требованиям технической документации. Конечно, качество сборки пары скольжения из этих деталей будет (по Тагути) значительно ниже, чем сборки этой пары из подобранных деталей. Трудоемкость сортировки деталей по калибрам не представляется большой, что не должно привести к серьезному удорожанию технологических процессов. К тому же стоимость сортировки можно ввести в стоимость сборки пары скольжения с меньшей величиной зазора, как более качественной.
Какие выводы можно сделать на основе выше изложенного:
1. Фактически Г. Тагути предлагает отменить принцип взаимозаменяемости, в основе которого лежит допуск, и вернуться в ремесленное производство, отличающееся индивидуальной подгонкой размеров деталей [33]. Очевидно, что индивидуальная подгонка позволяет получить оптимальные размеры деталей, которые, в свою очередь, обеспечивают точность соединений. С одной стороны, подгонка не способствует повышению производительности работ, но с другой – значительно повышает качество посадок соединения. Подход, предложенный Тагути, может в перспективе привести к резкому повышению точности сборки и созданию высококачественных изделий.
2. Применение функции потерь качества (по Тагути) позволяет получить экономическую оценку качества замыкающего звена сборочной размерной цепи не только по точности соединения (величине допуска), но и в зависимости от схемы расположения номинального размера замыкающего звена относительно координаты середины поля его (допуска).
3. Величина потерь качества среднего статистического показателя распределения Sσ зависит как от вида распределения, так и положения номинального размера параметра относительно координаты середины поля рассеяния.
4. Оценка потерь качества среднестатистического показателя распределения Sσ детали должна проводиться не автономно, а с учетом положения этой детали в размерной цепи.
5. На величину потерь качества в большей степени влияет не величина поля рассеяния, а положение координаты середины поля рассеяния относительно номинального размера параметра.
6. Схема расположения поля допуска относительно номинального размера параметра детали влияет на потери качества только замыкающего звена в размерной цепи.
7. Проведение мероприятий по увеличению точности технологической системы с целью уменьшение поля рассеяния случайного значения параметра и сокращения доли брака может оказаться неэффективным, если не будет учтено положение этого поля рассеяния относительно номинального значения параметра в реальной размерной цепи. Это замечание имеет особое отношение к методу «Шесть сигм».