
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Внутренняя функция потерь качества
|
|
Японский ученый Г. Тагути был первым, кто не согласился с традиционным положением, что попадание значения исследуемого параметра изделия в поле допуска является гарантией обеспечения требуемого качества, и показал, что потери качества не имеют место только в том случае, если значения параметра Х совпадают с номинальным значением параметра Хо. В остальных случаях (|Х - Хо| > 0) имеют место потери качества, в том числе и в поле допуска.
Г. Тагути считает, что потери качества пропорциональны квадрату разности (Х-Хо)², то есть чем больше отклонение показателя качества изделия от номинального его значения, тем серьезнее могут быть результаты отказа. На наш взгляд, это допущение экономически оправдано, если рассматривать в качестве потерь качества ущерб (значительно больший, чем стоимость затрат на эту деталь или сборку), который может быть нанесен изделию в результате отказа по вине данной детали (сборки).
Нас же в данном разделе интересуют не потери качества в связи с отказом изделия, а внутренние потери качественного состава значений параметра по мере их отклонения от номинала.
Общеизвестно, что с уменьшением допуска на параметр (показатель качества) детали растет его точность, а значит и качество изготавливаемого изделия. Значение точности определяется квалитетом. Если проанализировать поле рассеяния измеренных значений параметра детали при ее массовом изготовлении в заданный размер по 7-му квалитету точности, то можно выделить ряд измеренных значений, которые попали в 7-й, 6-й, 5-й и в другие более точные квалитеты. То есть можно провести селективную выборку изготовленных деталей по квалитетам точности и отобрать наиболее качественные. Очевидно, что сборки (узлы, изделия) из этих деталей будут тем качественнее, чем ниже номер квалитета. Значит, при изготовлении любой детали в заданный размер по какому-то N-у квалитету точности всегда можно найти внутри поля допуска более качественные детали, чем те, которые соответствуют именно этому квалитету. В этом случае потери качества случайного значения параметра происходят не обязательно в квадратичной степени расстояния до номинального размера, а в какой-то степени от изменения номера квалитета точности в поле рассеяния.
Таким образом, для определения внутренней функции потерь качества необходимо ответить на два основных вопроса [27, 28]:
- какое количество случайных значений параметра (показателя) качества, распределенного по соответствующему закону, попадает в заданный квалитет точности,
- какой вид должна иметь зависимость стоимости качества случайного значения параметра (показателя) качества от номера квалитета точности.
Начнем с решения первой задачи – выявить вероятность Р (Х) попадания случайных значений параметра при нормальном его распределении в поле интервала соответствующего квалитета точности значений параметра.
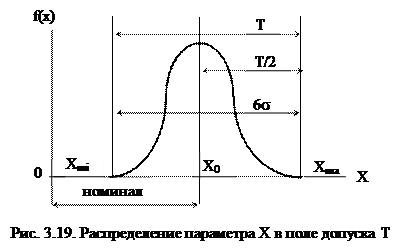
В качестве объекта исследования выбираем нормальное распределение значений параметра Х в поле его допуска Т, соответствующего 8-му квалитету точности. При этом координаты середина поля рассеивания и середины поля допуска совпадают. Номинальное значение параметра Хо = 100 мм, допуск Т= 54 мкм и симметрично расположен относительно номинального значения параметра. Поле рассеивания, равное 6σ, вписано в поле допуска (рис. 3.19), где σ – среднеквадратическое отклонение параметра Х.
Разделим каждую половину поля допуска исследуемого параметра (начиная от номинала) на диапазоны, соответствующие половине допуска всех нижестоящих (а их девять) квалитетов точности (табл. 3.12). Определим вероятность Р(Хk < Х < Хo) попадания соответствующих значений параметра Х в поле рассеяния в диапазонах Хk-Хo, где Хk – граница симметричного поля допуска к-го квалитета (к = 1, 2, …10):
1 хk (Хk – Хo)²
P(Хk -Хo) = ─ ─ ─ ─ ∫ exp[- ─ ─ ─ ─ ─ ─ ]dx.
σ √ 2π хо 2σ ² 
Запишем в табл. 3.12 значения вероятностей P(Xk –Хo) для всех десяти квалитетов точности. График вероятности P(Xk – Хo) по данным таблицы изобразим на рис. 3.19.
 |
Если допустить, что самые качественные значения параметра Х совпадают с координатой номинального размера параметра, то величина разности между 0, 5 и вероятностью Р(Х< Хо) свидетельствует о потерях качественного состава значений параметра Х. Очевидно, что чем больше Х, тем меньше осталось значений параметрах Х с хорошим качеством. Назовем эту разность функцией потерь качественного состава значений параметра Ф(Х):
Ф(Х) = 0, 5 – Р(Х - Хо).
Вычислим Ф(Х) и занесем результаты вычислений в табл. 3.12, а график функции Ф(Х) отразим на рис. 3.20.
Таблица 3.12
Значения внутренней функции Ф(Х)
| Номер квалитета | Допуск, мкм | Вероятность Р(Хk< Х< Хo) | Функция Ф(Х) |
| ±0, 5 ±0, 75 ±1, 25 ±2 ±3 ±5 ±7, 5 ±11 ±17, 5 ±27 | ±0, 022 ±0, 033 ±0, 055 ±0, 088 ±0, 1305 ±0, 2105 ±0, 2975 ±0, 389 ±0, 474 ±0, 4985 | ±0, 478 ±0, 467 ±0, 445 ±0, 412 ±0, 370 ±0, 290 ±0, 203 ±0, 111 ±0, 026 ±0, 0014 |
Вместе с этим функция Ф(Х) не является экономической функцией потери качества, так как отражает не стоимость потерь, а относительное (в %) ухудшение качественного состава значений параметра. Следует также обратить внимание на то, что внутренняя функция Ф(Х) на границах допуска Т совпадает с разрывной функцией потерь. За границами поля допуска внутренняя функция Ф(Х) отвечает традиционным понятиям о потере качества параметра с вероятностью соответствующей положению поля рассеяния в поле допуска (в нашем случае потери качества на границе допуска составляют 99, 73 %).
|

Перейдем к решению первой задачи: определение стоимости качества случайного значения параметра в зависимости от его положения в поле рассеяния, то есть от номера квалитета точности. Для решения этой задачи необходимо предварительно исследовать изменение трудоемкости изготовления деталей в зависимости от точности изготовления.
Проведем это исследование на примере обработки резанием наружной поверхности валика диаметром 32 мм и длиной 100 мм из стального прутка. Очевидно, что при невысоких квалитетах точности обработка будет проводиться точением, а с увеличением требований к точности – шлифованием. Как известно из технологии машиностроения, изготовление деталей высокой точности производится путем последовательного применения более точных операций обработки.
В соответствии с [52] точением можно изготавливать детали с 14 до 8-го квалитета точности в три стадии: черновое точение (14-12 квалитеты), получистовое точение (11 квалитет), чистовое точение (9-8 квалитеты).
Изготовление шлифованием деталей высокой точности проводится так же в три стадии: предварительное шлифование (9-8 квалитеты), чистовое шлифование (7-6 квалитеты), тонкое шлифование (6-5 квалитеты). Далее идет предельно возможная по точности механическая операция – суперфиниш (5-4 квалитеты).
Из справочного пособия по общемашиностроительным нормативам времени [52] выбираем для каждой стадии обработки точением величину неполного штучного времени при обработке цилиндрической поверхности установленного диаметра и длины. Именно неполное штучное время (без вспомогательного и подготовительно-заключительного) характеризует прямые затраты времени на соответствующую точность обработки. Занесем в табл. 3.13 нормативное время обработки поверхности заданного квалитета точности и соответствующей шероховатости поверхности.
Таблица 3.13
Неполное и накопленное штучное время обработки точением
| Стадия точения | Квалитет точности | Шероховатость поверхности | Неполное шт. время операции, мин | Накопленное шт время, мин |
| Черновое Получистовое Чистовое | 14-12 9-8 | Rz 80 – Rz 40 Rz 20 Ra 2, 5 – Ra 1, 25 | 0, 65 0, 54 0, 76 | 0, 65 1, 19 1, 95 |
Характер зависимости затрат накопленного времени на обработку поверхностей соответствующей точности отразим на рис. 3.21.
|
|
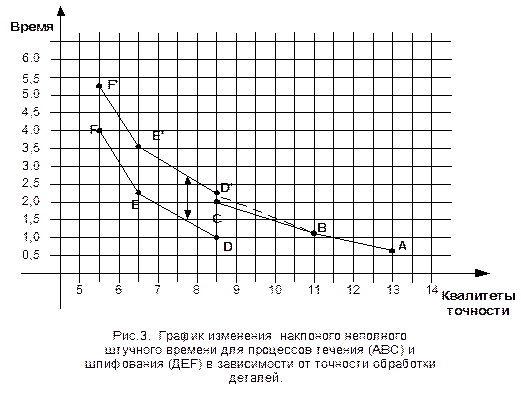
Аналогичные вычисления проведем при оценке накопленного времени шлифовальных операций по обработке наружной поверхности валика по общемашиностроительным нормативам времени на шлифовальных станках [52]. Результаты расчетов занесем в табл. 3.14, а характер зависимости накопленного времени при шлифовании – на рис. 3.21.
Если принять во внимание, что обработка шлифованием в квалитет 9-8 проводилась после получистового точения (накопленное неполное время 1, 19 мин), то накопленное неполное штучное время после предварительного шлифования составило 2, 22 мин, что незначительно (в пределах 10%) отличается от накопленного времени чистового точения (1, 95 мин). С учетом изложенного можно допустить совмещение точек Д' и С на графиках накопленного неполного штучного времени операций точения и шлифования (рис. 3.21). Такое допущение тем более правомерно, что стоимость работ по обработке точением и шлифование практически одинакова [52]: один час работы на токарно-винторезных станках (1К62, 16К20, 1М61) стоит от 515 до 546 руб., а на круглошлифовальных станках (3У102, 3А110В, 3У12) – от 587 до 638 руб.
Таблица 3.14
Неполное и накопленное штучное время при шлифовании
| Стадия шлифования | Квалитет точности | Шероховатость поверхности | Неполное шт. время операции, мин | Накопленное шт время, мин |
| Предварительное Чистовое Тонкое | 9-8 7-6 6-5 | Ra 2, 5 – Ra 1, 25 Ra 1, 25 – Ra 0.63 Ra 0, 63 | 1, 02 1, 30 1, 63 | 1, 02 2, 32 3, 95 |
Для выявления зависимости между стоимостью обработки поверхностей деталей и их точностью в диапазоне от 14 до 5-го квалитета сделаем допущение, что стоимость обработки резанием пропорциональна значению накопленного штучного времени. Выразим относительную стоимость механической обработки заданной поверхности в условных единицах (у. е.). Принимаем за одну условную единицу стоимость обработки поверхности по 11-му квалитету точности.
На основании характера изменения зависимостей неполного штучного времени от номера квалитета (рис. 3.21) методами регрессионного анализа было выведено уравнение зависимости стоимости обработки QN (в у. е.) от порядкового номера квалитета N (порядковый номер квалитета отличается от истинного номера квалитета точности на две единицы, учитывая, что первые два квалитета имеют номера 0 и 01):
QN = 102 exp (-0, 36 • N) у. е. (3.15)
В уравнении (3.15) одной условной единице соответствует стоимость обработки поверхности в 13-й порядковый квалитет (11-й фактический). Стоимость обработки поверхности в расчете на единицу квалитета можно назвать единичной стоимостью качества. Таким образом, можно считать QN – функция стоимости качества единичного измерения по N (порядковому) квалитету точности.
С целью проверки универсальности предлагаемой математической модели исследована возможность использования зависимости QN для других видов обработки. Адекватность выражается в сходимости соотношений накопленной трудоемкости (или относительной стоимости) при одних и тех же квалитетах точности как по уравнению (3.15), так и по нормативным данным. Результаты исследований показали, что уравнение (3.15) является универсальным для всех видов обработки резанием [27].
Уравнение (3.15) справедливо для единичного измерения, в то время как целью настоящей работы является оценка потерь качества (в стоимостном выражении) для всей совокупности значений исследуемого параметра, находящихся в поле допуска.
Очевидно, что стоимость качества распределения значений параметра поверхности (диаметр) деталей, находящихся в поле допуска конкретного квалитета точности, будет определяться произведением количества значений в поле допуска на стоимость качества (в нашем случае относительную) одной детали данного квалитета.
Определим относительную стоимость качества деталей разных квалитетов точности. При этом разделим всю совокупность значений исследуемого параметра, находящихся в поле максимального допуска, на группы значений размеров параметра, находящиеся в поле только собственного допуска (без включения в этот допуск значений параметра меньших квалитетов). Результаты вычислений занесем в табл. 3.15 в которой выделим следующие графы: графа 1 – названия (а не номера) квалитетов, графа 2 – симметричные допуски квалитетов, графа 3 – доли значений размеров деталей, входящие в допуск данного квалитета, графа 4 – доли значений размеров деталей, входящие в собственный допуск квалитета, графа 5 – относительная стоимость качества деталей в допуске данного квалитета, графа 6 – относительная стоимость качества деталей в допуске собственного квалитета, графа 7 – накопленная относительная стоимость качества деталей всех предшествующих квалитетов.
Таблица 3.15
Сводная таблица относительной стоимости качества
в разных квалитетах точности
| ±0, 5 ±0, 75 ±1, 25 ±2 ±3 ±5 ±7, 5 ±11 ±17, 5 ±27 | ± 0, 022 ± 0, 033 ±0, 055 ±0, 088 ±0, 1305 ±0, 2105 ±0, 2975 ±0, 3885 ±0, 474 ±0, 4985 | ± 0, 022 ± 0, 011 ±0, 022 ±0, 033 ±0, 042 ±0, 080 ±0, 087 ±0, 091 ±0, 085 ±0, 025 | 72, 1 50, 2 35, 0 23, 7 16, 5 11, 5 8, 0 5, 6 3, 9 2, 7 | ±1, 585 ±0, 55 ±0, 77 ±0, 78 ±0, 70 ±1.00 ±0, 70 ±0, 51 ±0, 35 ±0, 065 | ±1, 585 ±2, 135 ±2, 905 ±3, 685 ±4, 385 ±5, 385 ±6, 085 ±6, 595 ±6, 945 ±7, 010 |
Таким образом, из графы 7 и строки 8 видно, что накопленная относительная среднестатистическая стоимость качества детали в поле допуска 8-го квалитета при нормальном законе распределения значений исследуемого параметра составляет 14, 02 у. е. Абсолютная стоимость качества в условных единицах может быть рассчитана при известном общем количестве деталей n, попавших в поле допуска:
QΣ = n∙ QN = 14, 02· n.
Функция потерь относительной стоимости качества в поле допуска графически изображена на рис. 3.22. Как видно из графика, не наблюдается квадратичной зависимости потерь при отклонении значений параметра от номинального его значения. Такой зависимости и не может быть, так как стоимость качества деталей по мере приближения к границам максимального допуска (в нашем случае допуска 8 квалитета точности) снижается, а не возрастает.
Самые большие потери качества приходятся на допуски точных квалитетов, располагаемых в непосредственной близости от номинального значения параметра. Кривая потерь качества может быть только постепенно убывающей, но не постепенно возрастающей.
|

С изменением закона распределения значений исследуемого параметра
изменяются доли деталей, располагаемые в допусках внутренних квалитетов, и изменяется функция потерь качества. Нами рассчитаны накопленные относительные среднестатистические стоимости качества детали и при других законах распределения: при треугольном законе распределения QN = 11, 76 у.е., а при равномерном законе распределения QN = 7, 86 у.е.
На рис. 3.22 изображены графики функции потерь относительной стоимости качества QN как при равномерном распределении (кривая 3), так и при распределении по треугольнику (кривая 2). Совершенно естественно, что накопленная относительная стоимость качества деталей при этих законах распределения меньше, чем при нормальном законе распределения.
Полученные выше результаты по исследованию внутренней функции потерь качества показывают, что при массовом изготовлении деталей по 8-му квалитету точности в поле рассеяния значений распределения параметра можно выделить достаточно многочисленные группы деталей более высоких квалитетов (например, по 6-му квалитету – не менее 77%, по 4-му квалитету – не менее 42%).
Может оказаться экономически выгодным при большой вариабельности технологической системы не тратить средства на повышение точности системы, а отбирать детали повышенной точности. Их доработка до требуемой шероховатости обрабатываемых поверхностей не представляет большой технической сложности. Можно провести селективную выборку деталей по группам более высокой точности и собирать ответственные для эксплуатации изделия узлы. Очевидно, что более качественные детали позволят собирать более надежные узлы, которые должны иметь повышенную потребительскую ценность.
Так как каждая группа деталей входит в пределы требуемого допуска, то проблем взаимозаменяемости в группах не должно быть. Следует также отметить, что отходов при селекции не будет, так как все изготовленные детали соответствуют техническим требованиям по точности.
На наш взгляд, общепризнанные достоинства метода «Шесть сигм» связаны не столько с отсутствием брака изготовленной продукции (не такой уж он высок и при традиционной точности технологической системы – 99, 73%), сколько с получением групп деталей повышенного качества, из которых собираются узлы повышенной надежности.
3.6. Стратегия «Шесть сигм»
Вариабельность технологической системы является главным фактором отклонений отдельных значений параметра от требований технической документации. В качестве критерия оценки вариабельности технологической системы обычно применяется индекс воспроизводимости процесса Ср:
Cр = Т / 6σ,
где Т – допуск на параметр,
σ – среднеквадратическое отклонение распределения.
Традиционно в практике производства технологический процесс считается нормальным, если индекс воспроизводимости Ср находится в диапазоне от 1 до 1, 33. В то же время новый метод «Шесть сигм» обеспечивает индекс воспроизводимости более 1, 33. Что же скрывается за этим методом [4, 11, 59, 65, 69]?
В 1981 году Б. Гелвин, президент фирмы Motorola, поставил перед своими специалистами задачу: достичь десятикратного повышения производительности в течение пяти лет. Специалисты начали искать способы снижения потерь. Одному из инженеров фирмы, Б. Смиту, было поручено изучить корреляцию между поведением изделия в эксплуатации и частотой его отказов в процессе производства. Смит обнаружил следующую закономерность: если изделие отбраковывалось и дорабатывалось в процессе производства до товарного состояния, то вероятность его безотказной работы у потребителя снижалась из-за скрытых дефектов, не обнаруженных во время производства. Если же изделие было собрано с первого раза без отклонений от документации, то вероятность его исправной работы у потребителя возрастала. Одновременно, при изучении опыта ведущих фирм было установлено, что лучшие по надежности изделия создаются на тех фирмах, в которых процессы производства протекают с минимальным числом отказов. То есть надо изготавливать продукцию без отклонений от документации, для чего требуется повысить стабильность и точность технологической системы. Метод «Шесть сигм» впервые был испробован на фирме Motorola и сразу получил большой резонанс.
В начале 90-х годов прошлого столетия группа ведущих американских корпораций с учетом опыта фирмы Mоtorola провозгласила стратегию «Шесть сигм», направленную на повышение рентабельности продукции и улучшения удовлетворенности потребителей [75]. Стратегия «Шесть сигм» основана на том, что существует прямая корреляция между числом дефектов продукции и уровнем удовлетворенности потребителей. В концепции «Шесть сигм» общим показателем служит число дефектов на единицу продукции, допущенных на всех стадиях ее производства от поставки сырья и материалов, изготовления деталей, процесса сборки и до заполнения финансовых документов, расчета экономических показателей, планирования сроков поставки продукции потребителю и затрат на транспортировку.
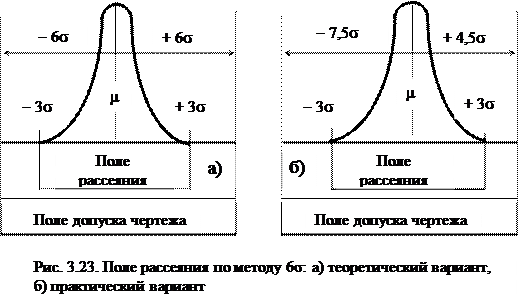
В основе концепции «Шесть сигм» заложен постулат, что в установленном допуске Т на конкретный параметр А среднеквадратическое отклонение распределения σ составляет 1/12 допуска. Это означает, что поле рассеяния значений параметра равно половине допуска. Очевидно, что чем больше сигм, тем менее вероятно, что будет допущен дефект, тем реже возникают отказы процесса, выше надежность продукта, ниже потребность в контроле и испытаниях, меньше незавершенного производства, ниже затраты и время производственного цикла и, как результат, – выше удовлетворенность потребителей.
Метод «Шесть сигм», в отличие от первоначальной концепции Ср =2, базируется на том, что удовлетворяющему данному критерию процессы допускают не более 4-х дефектов на миллион изделий. Строго говоря, эта дефектность и условие Ср = 2 не соответствуют друг другу, так как последнему условию соответствует уровень дефектности 2ррВ, т. е. два дефекта на миллиард изделий [75]. Такое несоответствие определяется тем, что в рамках метода «Шесть сигм» принимается, что центр распределения значений параметра не совпадает с координатой середины поля допуска, а может смещаться относительно него в ту или иную сторону на 1, 5σ (рис. 3.23). Это означает, что в практических условиях создать технологическую систему с индексом воспроизводимости Ср = 2 одновременно с условием нулевого смещения середины поля рассеяния от середины поля допуска невозможно.
.
 |
В табл. 3.16 приведены данные по соответствию числа σ и уровню дефектности.
Таблица 3.16
Зависимость числа дефектов от числа σ
| Число σ | Число дефектов на миллион, ррМ | Процент возможных издержек на качество | Примечание |
| 3, 4 | Мировой класс | ||
| 10-15 | |||
| 15-20 | Средний уровень | ||
| 20-30 | |||
| 30-40 | Недопустимый уровень | ||
Учитывая исключительно редкую практику применения метода «Шесть сигм» на российских предприятиях, рассмотрим на примере опыта обучения (на английском языке) этому методу специалистов ОАО «АВИСМА титано- магниевый комбинат» и «ВСМПО» (г. Верхняя Салда, Свердловская область) основное содержание учебного курса, который состоял из пяти этапов: определение дефектов, измерение, анализ, улучшение, контроль.
В этапы включены известные статистические методы, такие как метод Парето, диаграмма Исикава, распределение Пуассона, функция потерь качества Тагути, метод FMEA и др. Рассматривались схемы процессов типа: DMAIC (определять, измерять, анализировать, улучшать, контролировать), DVADV (определять, измерять, анализировать, проектировать, проверять), SIPOC (поставщики, входы, проект, выходы, потребители), QFD (развертывание функции качества).
Во время обучения группы разбиваются на команды, с которыми проводят практические занятия и выполняют статистические расчеты. Большое внимание уделяется психологическому климату в команде, умению распределять функции между ее членами и выявлять лидера. В процессе обучения большое внимание уделяется деловым играм по темам: «Планирование эксперимента» и «Анализ рисков». Много игр проводится по статистическим методам.
Философию обучения можно свести к следующим принципам:
- эффективное внедрение метода «Шесть сигм» возможно только при заинтересованности первого руководителя компании,
- этот метод нужен тебе, твоей компании и вашему потребителю,
- результат можно достигнуть, только работая в команде,
- необходимо все измерять и анализировать,
- любой процесс стоит денег.
Кому и что дает стратегия «Шесть сигм»:
- потребителям – обеспечивает более высокое качество и низкие цены,
- акционерам – дает возможность повысить доходы,
- поставщикам – дает возможность получить новые средства достижения успеха,
- сотрудникам – открывает более широкие возможности в работе и дает чувство гордости за выполняемую работу.
В ходе внедрения метода «Шесть сигм» на фирме Motorola были найдены оригинальные способы мотивации персонала: присвоение работникам, прошедшим обучение (по применению принципов «Шесть сигм» на практике), поясов разного цвета по аналогии с мастерами каратэ. Перечень лиц, кого условно можно назвать агентами «6 сигм», выглядит следующим образом: чемпионы, черные пояса, зеленые пояса, желтые пояса. Нас больше интересует перечень учебных курсов, которые преподавали на фирме:
- введение в статистическое управление процессами (SPC),
- идентификация, сбор и визуализация данных,
- гистограммы,
- диаграммы Парето,
- анализ с помощью диаграмм «причина-результат»,
- многомерный анализ,
- cтатистика I (для инструментов SPC до и после эксперимента: воспроизводимость процессов; контрольные карты; анализ измерительных систем),
- статистика II (для планирования эксперимента и их анализа: сравнительный анализ; факторный анализ; дробный факторный анализ; компонентный анализ; проектирование для обеспечения технологичности).
Полный курс обучения был рассчитан на 112-146 учебных часов, из которых примерно половина времени посвящена программе обучения методам планирования эксперимента. Следует отметить, что в литературе нет рекомендаций по стандартной программе обучения методу «Шесть сигм».
Многие фирмы в США, внедрившие метод «Шесть сигм» отмечают исключительно высокую рентабельность производства. Но, вместе с этим, в победных реляциях не всегда можно найти причины эффективности результатов. Это вызвало в адрес метода «Шесть сигм» много критических статей в журнале «Европейское качество» («European Quality»), авторы которых не увидели принципиальной новизны новой концепции.
Попробуем разобраться, в чем главные достоинства применения метода «Шесть сигм» и в чем его недостатки. Прежде о достоинствах.
1. Практически полное отсутствие дефектов, приводящих к браку продукции или ее доработке до товарного вида; снимает проблему потерь от несоответствующего качества и позволяет снизить себестоимость продукции и повысить ее конкурентоспособность.
2. Нулевая дефектность значительно поднимает рейтинг (имидж) компании в глазах потребителя и увеличивает привлекательность ее продукции.
3. Значительно снижаются потери качества (по Тагути) элементов продукции (см. п. 3.4 «Функции потерь качества по Тагути») при условии отсутствия или небольших смещениях координаты центра поля допуска от центра поля рассеяния параметра.
4. Уменьшение почти в два раза поля рассеяния параметра по сравнению с традиционными методами обеспечения точности позволяет изготавливать детали высоких квалитетов точности (см. п. 3.5 «Внутренняя функция потерь качества»). Более качественные детали обеспечивают сборку высоконадежных изделий.
Первый и второй пункты достоинств метода широко известны, но третий и четвертый пункты в литературе практически не упоминаются. Достоинства метода «Шесть сигм» именно по этим (последним двум) пунктам, на наш взгляд, является причиной получения высоких дивидендов от применения данного способа, так как выигрыш в первом пункте при невысокой дефектности продукции и при традиционных методах обеспечения качества не настолько велик, чтобы добиться значимой экономической эффективности.
Если в любом случае есть достоинства метода по первому пункту, то почему не все фирмы, внедрившие метод «Шесть сигм», получили значительный экономический выигрыш? Это связано с явными и неявными, на сегодняшний день, недостатками метода «Шесть сигм».
1. Внедрение метода «Шесть сигм» требует значительных затрат, как на обучение персонала, так и, главным образом, для приведения технологической системы по большому числу важнейших показателей качества к требуемой точности.
2. Потери качества (по Тагути) при изготовлении отдельной детали могут быть достаточно большими даже при малом поле рассеяния параметра, если середина поля допуска не совпадает с координатой номинального размера (см. п. 3.4 «Функции потерь качества по Тагути»).
3. Качество изделия зависит не столько от качества изготовления входящих в него деталей, сколько от качества замыкающего звена размерной цепи изделия. Особенно сложно обеспечить качество замыкающих звеньев малозвенных размерных цепей. При многозвенных размерных цепях, даже при небольшом поле рассеяния замыкающего звена, значительные потери качества могут возникнуть при неблагоприятном положении (несовпадении) номинального размера относительно середины поля допуска звена. При этом потери качества могут быть вызваны попаданием большей части размеров замыкающих звеньев в невысокие квалитеты точности (см. п. 3.5 «Внутренняя функция потерь качества»).
В целом при оценке метода «Шесть сигм» можно согласиться с тем, что ведущие мировые фирмы при внедрении этого метода делают акцент не столько на малое число дефектов на миллион возможностей, сколько на стратегию системного снижения вариабельности процессов.