
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Отклонение случайной величины от се математического ожидания
|
|
Лекция 11
ДИСПЕРСИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
1. Целесообразность введения числовой характеристики
рассеяния случайной величины
Легко указать такие случайные величины, которые имеют одинаковые математические ожидания, но различные возможные значения. Рассмотрим, например, дискретные случайные величины X и У, заданные следующими законами распределения:
| X | – 0, 01 | 0, 01 | Y | –100 | ||
| p | 0, 5 | 0, 5 | p | 0, 5 | 0, 5 |
Найдем математические ожидания этих величин: М(X) = – 0, 01*0, 5 + 0, 01*0, 5 = 0, M(Y) = –100*0, 5 + 100*0, 5 = 0.
Здесь математические ожидания обеих величин одинаковы, а возможные значения различны, причем X имеет возможные значения, близкие к математическому ожиданию, а Y – далекие от своего математического ожидания. Таким образом, зная лишь математическое ожидание случайной величины, еще нельзя судить ни о том, какие возможные значения она может принимать, ни о том, как они рассеяны вокруг математического ожидания. Другими словами, математическое ожидание полностью случайную величину не характеризует.
По этой причине наряду с математическим ожиданием вводят и другие числовые характеристики. Так, например, для того чтобы оценить, как рассеяны возможные значения случайной величины вокруг ее математического ожидания, пользуются, в частности, числовой характеристикой, которую называют дисперсией.
Прежде чем перейти к определению и свойствам дисперсии, введем понятие отклонения случайной величины от ее математического ожидания.
Отклонение случайной величины от се математического ожидания
Пусть X – случайная величина и M(X) – ее математическое ожидание. Рассмотрим в качестве новой случайной величины разность Х – М(Х).
Отклонением называют разность между случайной величиной и ее математическим ожиданием.
Пусть закон распределения X известен:
| X | x1 | x2 | … | xn |
| p | p1 | p2 | … | pn |
Напишем закон распределения отклонения. Для того чтобы отклонение приняло значение х1–М(Х), достаточно, чтобы случайная величина приняла значение х1. Вероятность же этого события равна р1, следовательно, и вероятность того, что отклонение примет значение х1–М(Х), также равна р1. Аналогично обстоит дело и для остальных возможных значений отклонения.
Таким образом, отклонение имеет следующий закон распределения:
| X–М(Х) | x1–М(Х) | x2–М(Х) | … | xn–М(Х) |
| p | p1 | p2 | … | pn |
Приведем важное свойство отклонения, которое используется далее.
Теорема. Математическое ожидание отклонения равно нулю:
М [Х–М(Х)] = 0.
Доказательство. Пользуясь свойствами математического ожидания (математическое ожидание разности равно разности математических ожиданий, математическое ожидание постоянной равно самой постоянной) и приняв во внимание, что М (X) – постоянная величина, имеем
М [X –М (X)] = М (X) – М [М (X)] = М (X) – М (X) = 0.
Пример 1. Задан закон распределения дискретной случайной величины X:
| X | ||
| р | 0, 2 | 0, 8 |
Убедиться, что математическое ожидание отклонения равно нулю.
Решение. Найдем математическое ожидание X:
М (X) = 1*0, 2 + 2*0, 8 = 1, 8.
Найден возможные значения отклонения, для чего из возможных значений X вычтем математическое ожидание M(Х): 1 –1, 8 = –0, 8; 2 – 0, 8 = 0, 2.
Напишем закон распределения отклонения:
| X– М(Х) | -0, 8 | 0, 2 |
| р | 0, 2 | 0, 8 |
Найдем математическое ожидание отклонения:
М [Х – М (Х)] = (- 0, 8)*0, 2 + 0, 2*0, 8 = 0.
Итак, математическое ожидание отклонения равно нулю, как и должно быть.
Замечание. Наряду с термином «отклонение» используют термин «центрированная величина». Центрированной случайной величиной 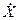 называют разность между случайной величиной и ее математическим ожиданием:
называют разность между случайной величиной и ее математическим ожиданием:
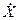 = Х – M(X).
= Х – M(X).
Название «центрированная величина» связано с тем, что математическое ожидание есть центр распределения.