Билет 7

1. Правило ваз Гиббса. Понятия: фаза, независимые компоненты, степени свободы, вариантность системы, равновесное состояние. К каким системам применимо правило фаз Гиббса? Определите вариантность системы на кривых ликвидуса в двухкомпонентной системе и объясните, что это значит.

Правило фаз Гиббса представляет собой математическую зависимость между числом степеней свобода (F), числом фаз (Р) и числом независимых компонентов (К) в системах, находящихся в равновесном состоянии. В общей форме правило фаз имеет вид:

F + р = k + m

m – число внешних параметров, влияющих на равновесие.

Фазой (Р) называется однородная часть системы с одинаковыми физическими, химическими и термодинамическими свойствами» которая отделена поверхностью раздела от других частей системы (от других фаз) и которую можно выделить из системы механическими средствами.

Под компонентами системы в общем смысле этого слова обычно понимают все те индивидуальные химические соединения, которые существуют в данной системе. Числом независимых компонентов называется минимальное число компонентов (соединений), с помощью которых, используя стехиометрические уравнения, можно выразись состав любой фазы системы.

Число независимых компонентов находится из выражения:

К = Коб - х, где Кобщ - общее число компонентов (соединений), а х - число стехиометрических уравнений реакций, которыми могут быть связаны все компоненты системы.

Например, в системе, состоящей из трех фаз: CaCO3, СaO и CO2, общее число компонентов (соединений) равно трем, однако число независимых компонентов К = 2, поскольку три указанных соединения могут быть связаны одним уравнением реакции СаСО3= СаО + СO2 (процесс разложения СаСO3), т.е. К = 3 - I = 2

Степень свободы (F) – независимые параметры системы, которые можно в определенных пределах изменять, не нарушая равновесия в системе, т.е. не изменяя числа и природы фаз.

Вариантность системы: система, которая не имеет степеней свободы называется инвариантной; с одной степенью свободы – моновариантная; с двумя – дивариантная и т.д.

Для систем, равновесие в которых зависит от давления: F=K-p+2; 2 учитывает температуру и давление.

Для систем с постоянными давлением: F=K-p+1.

Равновесное состояние: признаки: система в равновесном состоянии имеет минимальную энергию Гиббса; одинаковость параметров во всех точках системы; в равновесной системе число и природа фаз не изменяется в определенном интервале параметров.

2. Диаграммы состояния однокомпонентной системы в общем выражении в координатах р-Т. Элементы строения диаграммы, кривые упругости пара. Энантиотровные и монотропные превращения и их изображение на диаграмме. Правило ступеней Оствальда, примеры реализации этого правила в конкретных системах.

К элементам строения диаграмм состояния однокомпонентных систем относятся: координатные оси, линии упругости пара (пограничные линии), области стабильного существования отдельных фаз и тройные точки.

Линии упругости пара разделяют все поле диаграммы на области стабильного существования отдельных фаз, обозначение этих фаз указываются в соответствующих областях диаграммы.

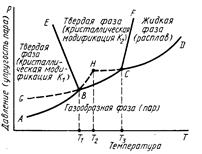
В полях система дивариантна, в равновесии одна фаза, т.е. можно изменять два параметра. На кривых упругости пара система моновариантна, в равновесии две вазы. В точках В и С система инвариантна, в равновесии три фазы.

Полиморфизм – способность соединения одного и того же химического состава существовать в различных структурах.

Полиморфные превращения: энантиотропные (обратимые) и монотропные (необратимые).

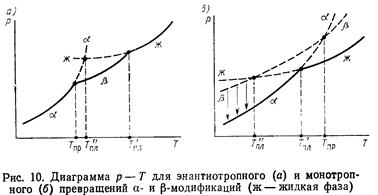
Правило ступеней Оствальда: образование вещества, существующего в нескольких полиморфных модификациях, протекает ступенчато таким образом, что сначала стремится образоваться неустойчивая (или менее устойчивая) форма с большей энергией Гиббса, которая затем при соответствующих условиях превращается в стабильную форму с минимальной энергией Гиббса.