Первая задача анализа на чувствительность (анализ на чувствительность к правой части ограничений)

Теоретическое введение

Неизбежное колебание значений таких экономических параметров, как цены на продукцию и сырье, запасы сырья, спрос на рынке и т.д. может привести к неоптимальности или непригодности прежнего режима работы. Для учета подобных ситуаций проводится анализ чувствительности, т.е. анализ того, как возможные изменения параметров исходной модели повлияют на полученное ранее оптимальное решение ЗЛП.

Для решения задач анализа чувствительности ограничения линейной модели классифицируются следующим образом. Граничные прямые связывающих ограничений проходят черезоптимальную точку. Граничные прямые несвязывающих ограничений не проходят черезоптимальную точку. Аналогично “ресурс”, представляемый связывающим ограничением, называют дефицитным, а “ресурс”, представляемый несвязывающим ограничением – недефицитным. Слово “ресурс” взято в кавычки, поскольку ограничения ЗЛП могут быть обусловлены не только ограниченностью действительных ресурсов, но и другими экономическими требованиями рассматриваемой задачи, например, условиями реализации продукции на рынке. В дальнейшем будем иметь это в виду и кавычки опустим. Ограничениеназывают избыточным в том случае, если его исключение не влияет на область допустимых решений (ОДР) и, следовательно, на оптимальное решение. Выделяют следующие три задачи анализа на чувствительность.

1. Анализ сокращения или увеличения ресурсов:

· на сколько можно изменить дефицитный ресурс для улучшения оптимального значения целевой функции (ЦФ)? Под улучшением оптимального значения ЦФ здесь понимается увеличение (уменьшение) этого значения в случае поиска максимума (минимума) ЦФ.

· на сколько можно изменить недефицитный ресурс (правую часть несвязывающего ограничения) при сохранении оптимального значения ЦФ?

2. Для какого из ресурсов изменение его “ запаса ” (т.е. правой части ограничения) наиболее выгодно?

3. Анализ изменения коэффициентов ЦФ: каков диапазон изменения коэффициентов ЦФ, при котором не меняется оптимальное решение?

Методика графического анализа чувствительности оптимального решения

Первая задача анализа на чувствительность (анализ на чувствительность к правой части ограничений)

Проанализируем чувствительность оптимального решения задачи №1 о производстве красок (см. Приложение 1, где поставлена эта задача и приведена ее математическая формулировка). ОДР задачи №1 (рис.1) – многоугольник ABCDEF. В оптимальной точке Е пересекаются граничные прямые (1) и (2). Поэтому ограничения (1) и (2) являются связывающими, а соответствующие им ресурсы (ингредиенты А и В) – дефицитными.

Рассмотрим экономический смысл этих понятий. Точка максимума ЦФ Е соответствует суточному производству т краски 1-го вида и т краски 2-го вида. В производстве красок используются ингредиенты А и В. Суточный запас на складе ингредиентов А и В – это правые части связывающих ограничений (1) и (2) (6 и 8 т ингр./сутки). Согласно этим ограничениям, на производство в точке Е расходуется

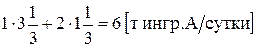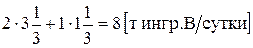(1) и (2).

Рис.1. Графическое решение задачи №1 о красках.

Таким образом, понятие " связывающие ограничения " (1) и (2) означает, что при производстве красок в точке 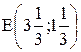запасы ингредиентов А и В расходуются полностью и по этой причине невозможно дальнейшее наращивание производства. В этом заключается экономический смысл понятия дефицитности ресурсов, т.е. если фирма сможет увеличить суточные запасы ингредиентов, то это позволит увеличить выпуск красок. В связи с этим возникает вопрос, до какого уровня целесообразно увеличить запасы ингредиентов и на сколько при этом увеличится оптимальное производство красок?