Метода №2

Чтобы численно определить новую величину запаса дефицитного ресурса, вызывающую улучшение оптимального решения,

необходимо: 1) определить координаты точки 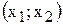, в которой соответствующее ограничение становится избыточным;

2) подставить координаты 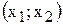в левую часть соответствующего ограничения; полученное значение и будет новой величиной исследуемого дефицитного ресурса.

Координаты точки К(3; 2) находятся путем решения системы уравнений граничных прямых ограничений (2) и (4). Т.е. в этой точке фирма будет производить 3 т краски 1-го вида и 2 т краски 2-го вида. Подставим 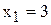и 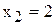в левую часть ограничения (1) и получим новую величину запаса ингредиента А

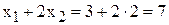[т ингр.А/сутки].

Дальнейшее увеличение запаса ингредиента А нецелесообразно, потому что это не изменит ОДР и не приведет к другому оптимальному решению (см. рис.2). Доход от продажи красок в объеме, соответствующем точке К, можно рассчитать, подставив ее координаты (3; 2) в выражение ЦФ

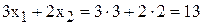[тыс.руб./сутки].

Рассмотрим вопрос о целесообразности увеличения запаса ингредиента В. Согласно методе №1, соответствующее ограничение (2) становится избыточным в точке J, в которой пересекаются прямая (1) и ось переменной 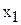(рис.3). Многоугольник ABCDJ становится ОДР, а точка J(6; 0) – оптимальным решением.

Рис.3. Анализ увеличения ресурса В.

В точке J выгодно производить только краску 1-го вида (6 т в сутки). Доход от продажи при этом составит

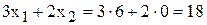[тыс.руб./сутки].

Чтобы обеспечить такой режим работы, согласно методе №2, запас ингредиента В надо увеличить до значения

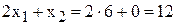[т ингр.В/сутки].

Ограничения (3) и (4) являются несвязывающими, т.к. их граничные прямые не проходят через оптимальную точку E (см. рис.1). Соответствующие им ресурсы (спрос на краски) являются недефицитными. С экономической точки зрения это означает, что в данный момент уровень спроса на краски непосредственно не определяет объемы производства. Поэтому некоторое его колебание может никак не повлиять на оптимальный режим производства в точке E.

Например, увеличение (уменьшение) спроса на краску 2-го вида будет соответствовать перемещению прямой ограничения (4) вверх (вниз). Перемещение прямой (4) вверх никак не может изменить точку Е максимума ЦФ. Перемещение же прямой (4) вниз не влияет на существующее оптимальное решение только до пересечения с точкой Е (см. Методу №3). Из рис.1 видно, что дальнейшее перемещение (4) приведет к тому, что точка Е будет за пределами новой ОДР, выделенной более темным цветом. Кроме того, любое оптимальное решение для этой новой ОДР будет хуже точки Е.