Метода №5

Чтобы определить границы допустимого диапазона изменения коэффициента ЦФ, например, и ,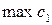

необходимо приравнять тангенс угла наклона целевой прямой 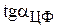поочередно к тангенсам углов наклона прямых связывающих ограничений, например 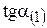и 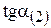(рис.5 и 6).

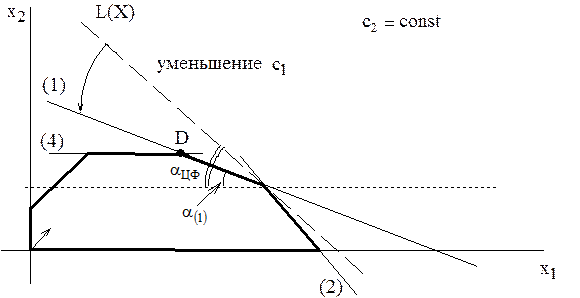
Рис.5. Определение .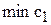

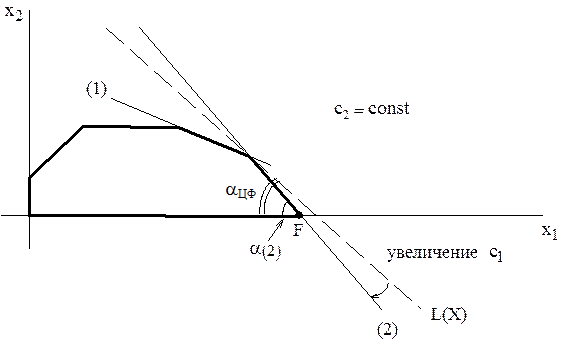
Рис.6. Определение .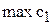

Определим, насколько максимально может снизиться цена на краску 1-го вида, не изменяя оптимальную точку Е. Для этого применим Методу №5 и формулу расчета тангенса угла наклона прямой (рис.7).

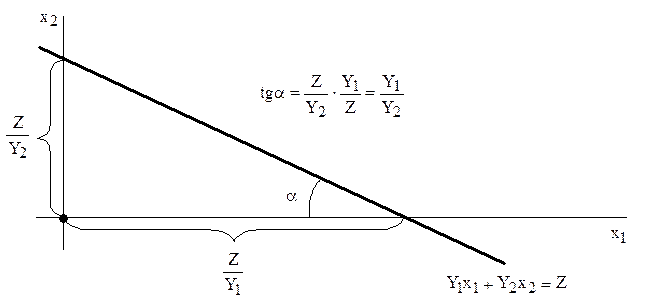
Рис.7. Определение тангенса угла наклона 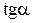прямой .

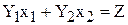Определим тангенсы углов наклона:

1) целевой прямой 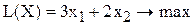, учитывая, что 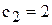фиксировано

;

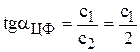2) граничной прямой связывающего ограничения 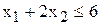(1)

;

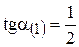3) граничной прямой связывающего ограничения 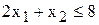(2)

.

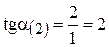Для нахождения min 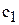целевая прямая должна совпасть с прямой (1) (см. рис.5):

;

;

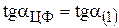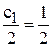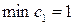[тыс.руб./т].

Для нахождения max 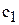целевая прямая должна совпасть с прямой (2) (см. рис.6):

;

;

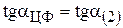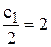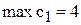[тыс.руб./т].

Таким образом, если цена на краску первого вида будет колебаться в пределах 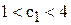тыс. руб./т (при фиксированной цене 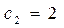тыс. руб./т), то оптимальное решение задачи не изменится.

Из приведенных выше расчетов и графической их иллюстрации следует, что если цена на краску первого вида станет меньше 1 тыс.руб./т (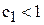 при фиксированной цене 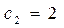тыс. руб./т), то наиболее выгодным будет производство красок в точке D (см. рис.5). При этом общее потребление ингредиента В снизится, что приведет к его недефицитности [ресурс (2)], а дефицитными будут ресурсы (1) и (4).