
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Средняя квадратическая величина
|
|
При условии подстановки значения k=2 в формулу (2) получаем
среднюю квадратическую величину. В ранжированном ряду она рассчитывается по невзвешенной (простой) форме:
x =√ ∑ x² /n (7)
где х — варианты ранжированного ряда; п — общее число вариант.
Порядок расчета средней квадратической простой величины заключается в следующем:
1.Каждая варианта ранжированного ряда возводится в квадрат (х2).
2.Квадраты вариант суммируются (∑ x2).
3.Сумму квадратов делят на общее число вариант в ранжированном ряду (∑ x² /n).
4. Из результата извлекают квадратный корень (√ ∑ x² /n), он представляет собой среднюю квадратическую величину для ранжированного ряда распределения.
Взвешенная форма средней квадратической величины, которая используется для дискретного или интервального ряда, выражается следующим образом:
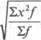
|
x =
Для расчета средней квадратической взвешенной величины применяется такой порядок:
1) все варианты ряда возводят в квадрат (х2);
2) квадраты взвешивают по соответствующим им частотам (частостям)-(x2 f);
3) взвешенные квадраты суммируют (∑ x2 f);
4) суммируют общее число вариант ((∑ f);
5) сумму взвешенных квадратов делят на общее число вариант(∑ x2 f /∑ f)
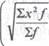
|
6) из полученного результата извлекают квадратный корень
что представляет собой среднюю квадратическую взвешенную величину.
Как самостоятельный вид средних она имеет ограниченное применение. Допустим, две нестандартные цилиндрические емкости для хранения нефтепродуктов с диаметрами оснований 2 и 5 м необходимо заменить двумя новыми, равными по объему емкостями с одинаковым в основании диаметром. При расчете среднего диаметра оснований новых емкостей по способу средней арифметической простой величины, т. е.
х = ∑ x/n =2 +5 /2 = 3, 5 м, результат оказывается заниженным, и по этому диаметру объемы новых емкостей будут меньше объемов имеющихся емкостей, что не соответствует условию задания. Дело в том, что площади оснований цилиндрических емкостей соотносятся между собой не линейно, а как квадраты их радиусов. Поэтому рассчитывать средний диаметр новых емкостей целесообразно по средней квадратической простой величине:

Таким образом, диаметр оснований новых емкостей должен быть не 3, 5, а 3, 8 м.
Если же исходные данные представлены в виде дискретного или интервального ряда, то целесообразно применить способ средней квадратической взвешенной величины. Например, необходимо рассчитать средний диаметр сосновых бревен по данным табл. 5.
Таблица 5. Число и размер бревен в штабеле
| Число бревен | Диаметр, см | |
| в вершине | в комле | |
| 10 20 30 10 | 25 35 45 55 | 55 65 |
Диаметр бревен (варианта) представлен в виде интервального ряда, при этом число их (частота) по каждой группе кратно 10. Это означает, что при расчете среднего диаметра бревен в штабеле можно воспользоваться вторым свойством средней величины и сократить частоту каждой группы в 10 раз. Средний диаметр бревен в штабеле рассчитываем по формуле (8), (табл. 6).
Таблица 6. Порядок расчета среднего диаметра бревен в штабеле
| Число бревен | Диаметр, см | Середина интервала (х), см | Квадраты диаметра (х2) | Взвешенные квадраты диаметра х2 f/10 | ||
| фактическое, шт. (f) | сокращенное f/10 | в в вершине | в комле | |||
| ∑ 70 | - | - | - | 1600 2500 3600 - | 900 3200 7500 3600 15200 |
С учетом применения второго свойства средних величин конечный расчет среднего диаметра бревен в штабеле принимает вид:

|
•
= √ 2171 =46, 5 см.
Таким образом, средневзвешенный диаметр сосновых бревен в штабеле, рассчитанный по способу средней квадратической величины, составляет 46, 5 см.
Главная сфера применения средней квадратической величины (в невзвешенной и взвешенной формах) — нахождение среднего квадратического отклонения.