
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Погрешности измерений и их классификация
|
|
Результаты измерений, вследствие несовершенства измерительных приборов, наших органов чувств и других независящих от нас причин, всегда содержат погрешность. Это значит, что в любом измерении мы получаем не истинное значение физической величины, а лишь близкое к нему. Теория погрешностей дает нам возможность установить предельное значение погрешности, определить интервал, в котором вероятнее всего находится истинное значение измеряемой величины.
Погрешность измерений – это отклонение результата измерения от истинного значения физической величины, т. е это разность между измеренным и истинным значениями измеряемой величины:
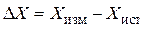 . (П3)
. (П3)
Погрешность, определённая такой формулой, называется абсолютной. Кроме абсолютной погрешности D X часто бывает важно знать относительную погрешность  , которая равна отношению абсолютной погрешности к истинному значению измеряемой величины и выражается в процентах:
, которая равна отношению абсолютной погрешности к истинному значению измеряемой величины и выражается в процентах:
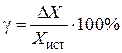 . (П4)
. (П4)
Относительная погрешность позволяет лучше характеризовать качество измерений, чем абсолютная. Например, одна и та же абсолютная погрешность в 1 мм при измерении длины комнаты не играет роли, а при определении диаметра болта совершенно недопустима. Ясно, что у этих измерений одинаковые абсолютные погрешности, но разные относительные. Как следует из формул (П3) и (П4), для нахождения абсолютной и относительной погрешности измерений нужно знать не только измеренное, но и истинное значение измеряемой величины. Что же такое истинное значение?
Истинное значение физической величины – это значение, которое идеальным образом отражало бы в качественном и количественном отношениях соответствующее свойство объекта. Но если истинное значение известно, то незачем производить измерения!
Итак, поскольку истинное значение физической величины неизвестно, то неизвестна и погрешность. Поэтому формулы (П3) и (П4) для практики непригодны. На практике погрешности не вычисляются, а оцениваются. Если истинное значение физической величины мы в состоянии знать только приближённо, то и погрешность тоже выражается приближённым значением. Для того, чтобы оценить достоверность измерений, требуется знать степень этого приближения, то есть требуется знать не только результат измерения и его погрешность, но также и вероятность того, что истинное значение измеряемой величины отличается от измеренного не более, чем на указанную погрешность.
Таким образом, корректно выполненные измерения должны иметь своим итогом: результат, погрешность и вероятность того, что отклонение измеренной величины от её истинного значения не превышает указанной погрешности.
В соответствии с ГОСТ 8.011 – 72, результат любого измерения Q должен быть представлен в форме:
 , P = …, (П5)
, P = …, (П5)
где X – результат измерения, выраженный в единицах измеряемой величины, D X – погрешность, выраженная в тех же единицах, P – установленная вероятность, с которой погрешность находится в этих границах.
Замечание о значащих цифрах. Значащими цифрами считаются все цифры числа, кроме крайних нулей, стоящих слева. Количество значащих цифр не всегда совпадает с количеством десятичных знаков после запятой, это разные вещи. Например, числа 784; 78, 4; 7, 84; 0, 784; 0, 0784; 0, 0000784 обладают одинаковым количеством значащих цифр. Для учебных целей будем оставлять в погрешности, как правило, одну значащую цифру. Исключения из этого правила будем делать, когда первая цифра погрешности равна единице. В этом случае будем оставлять в погрешности две значащие цифры. Конечный результат полагается округлять до того количества значащих цифр, которое диктует погрешность. Например, если результат получился X =26, 8964, а погрешность D X =0, 3, то результат следует округлить до X =26, 9 и записать Q =26, 9 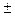 0, 3.
0, 3.
Погрешности бывают систематическими, случайными и грубыми.
Грубая погрешность измерений, или промах – это погрешность, существенно превышающая ожидаемую при данных условиях погрешность. Такие погрешности происходят либо по недосмотру оператора, либо из-за неисправности аппаратуры. Грубых погрешностей следует избегать. Если установлено, что они произошли, соответствующие измерения нужно отбрасывать.
Систематическая погрешность измерения – составляющая погрешности, которая остаётся постоянной или закономерно изменяется при повторных измерениях одной и той же физической величины. Она обозначается буквой q, например, q X.
Случайная погрешность измерения – составляющая погрешности, которая изменяется случайным образом при повторных измерениях одной и той же величины вследствие невозможности учесть многочисленные воздействия при измерении. Она обозначается буквой d, например, d X.