
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Графический способ оценки случайной погрешности
|
|
Пусть функция 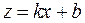 линейная или её можно свести к линейной. Случайные погрешности d k и d b можно определить графически.
линейная или её можно свести к линейной. Случайные погрешности d k и d b можно определить графически.
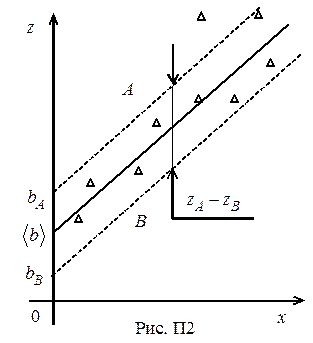 По экспериментальным точкам можно провести прямую наилучшего соответствия (рис. П2). Оценим случайную погрешность d b величины b. Для этого проведём параллельно экспериментальной прямой по обе стороны две прямые A и B по возможности ближе так, чтобы большинство точек, (кроме промахов) оказалось внутри. Тогда величину
По экспериментальным точкам можно провести прямую наилучшего соответствия (рис. П2). Оценим случайную погрешность d b величины b. Для этого проведём параллельно экспериментальной прямой по обе стороны две прямые A и B по возможности ближе так, чтобы большинство точек, (кроме промахов) оказалось внутри. Тогда величину 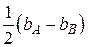 можно трактовать как интервал, равный 2 S – удвоенной выборочной средней квадратичной погрешности. Во внутрь этого интервала попадает не менее 95% измерений. С другой стороны, случайная абсолютная погрешность величины b равна (П8)
можно трактовать как интервал, равный 2 S – удвоенной выборочной средней квадратичной погрешности. Во внутрь этого интервала попадает не менее 95% измерений. С другой стороны, случайная абсолютная погрешность величины b равна (П8)
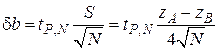 . (П23)
. (П23)
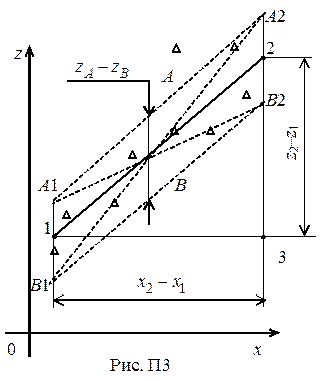 Для оценки случайной погрешности d k углового коэффициента k, среднее значение которого находится из треугольника 1–2–3 (рис. П3)
Для оценки случайной погрешности d k углового коэффициента k, среднее значение которого находится из треугольника 1–2–3 (рис. П3)
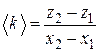 . (П24)
. (П24)
Проводят параллельно экспериментальной прямой 1–2 две линии A и B так, чтобы большинство точек оказалось внутри. Крайние точки B 1– A 2, A 1– B 2 соединяют крест-накрест. Это экспериментальные прямые, проведенные под максимально и минимально возможными углами. Их угловые коэффициенты:
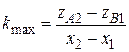 ,
,  . (П25)
. (П25)
Эти величины можно трактовать как наибольшее и наименьшее значение углового коэффициента k, отличающегося от среднего на величину 2 S. Тогда его случайная погрешность
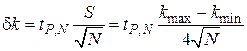 . (П26)
. (П26)
Можно упростить оценочную формулу, если подставить значения 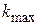 и
и  из (П25):
из (П25):
 , (П27)
, (П27)
здесь 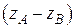 – расстояние между вспомогательными прямыми (рис. П3).
– расстояние между вспомогательными прямыми (рис. П3).
2. Правила построения и обработки графиков
График – самое наглядное представление результатов эксперимента. Графическое представление облегчает сравнение величин, позволяет легко обнаружить наличие характерных точек (экстремумов, точек перегиба), провести интерполяцию, экстраполяцию, обнаружить промах (рис. П4, П5).
1. График выполняется на миллиметровой бумаге размером с тетрадный лист (А5).
2. Прочертить координатные оси. Для независимой переменной (аргумента) используют ось абсцисс, для функции – ось ординат. Масштаб нужно выбирать так, чтобы экспериментальные точки заняли весь лист. Оси надо равномерно разметить и поставить числа напротив меток.
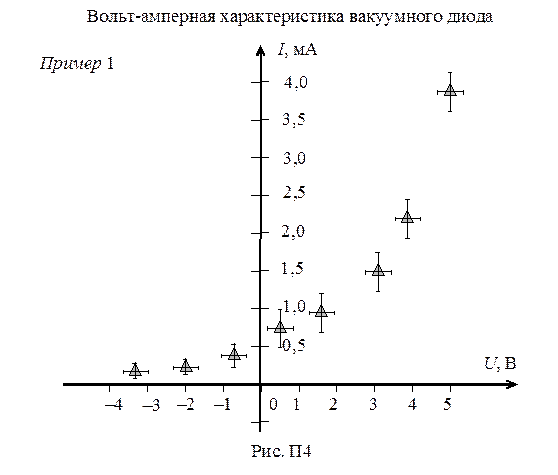 |
3. В конце оси указать откладываемую величину и её размерность, а также порядок масштаба (10±k, где k – целое число).
4. Экспериментальные точки на график нужно наносить тщательно и точно, обводя их каким-либо знаком:  ,
,  , □, +. Числа, соответствующие экспериментальным точкам, на осях не откладывать, т.к. это затрудняет работу с графиком. Если известны погрешности величин, то можно их указать на экспериментальной точке в виде креста, по горизонтали которого откладывают удвоенную погрешность аргумента, а по вертикали – удвоенную погрешность функции.
, □, +. Числа, соответствующие экспериментальным точкам, на осях не откладывать, т.к. это затрудняет работу с графиком. Если известны погрешности величин, то можно их указать на экспериментальной точке в виде креста, по горизонтали которого откладывают удвоенную погрешность аргумента, а по вертикали – удвоенную погрешность функции.
5. Экспериментальные точки не соединять. В некоторых случаях необходимо провести прямую наилучшего соответствия или теоретически рассчитанную кривую. Прямая должна быть проведена так, чтобы отклонения от неё соответствующих экспериментальных точек было минимальным. При этом число точек под прямой должно быть приблизительно равным числу точек над прямой.
6. Вверху необходимо написать название графика.

3. Правила вычислений
При проведении расчётов или измерений необходимо ограничиться разумной точностью. Результат записать так, чтобы значащие цифры, стоящие перед последней, были достоверны, т.е. разряд последней цифры был равен разряду погрешности измерений. При округлении результата следует пользоваться следующими правилами. Если округляемая цифра меньше 5, то ее просто отбрасывают; если больше 5, то к последней неотбрасываемой цифре прибавляют единицу; если равна 5 и за ней нет значащих цифр, то округляют до ближайшего четного числа. При записи значения больших или малых по порядку величин общепринято использовать множитель  , где k– целое число.
, где k– целое число.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Рязанов, Г.А. Опыты и моделирование при изучении электростатического поля / Г.А. Рязанов. – М.: Наука, 1966. – 200 с.
2. Калашников, С.Г. Электричество / С.Г. Калашников. – М.: Наука, 1983. – 576 с.
3. Сивухин, Д.В. Общий курс физики. Электричество / Д.В. Сивухин. – М.: Наука, 1983.– 688 с.
4. Трофимова, Т.И. Курс физики: учебное пособие для вузов / Т.И. Трофимова. – 5-е изд., стер. – М.: Высш. шк., 2006. – 352 с.
5. Лабораторные занятия по физике: учебное пособие / под ред. Л.Л. Гольдина. – М.: Наука, 1983. – 703 с.
6. Физический практикум / под ред. В.И. Ивероновой. – М.: Наука, 1968.– 325 с.
7. Корнфельд, М.И. Погрешность и надежность простейших экспериментов / М.И. Корнфельд // УФН. – 1965. – Т. 85. – С. 533.
8. Зайдель, А.Н. Погрешности измерения физических величин / А.Н. Зайдель. – Л.: Высшая школа, 1985. – 105 с.
9. Касандрова, О.Н. Обработка результатов измерений / О.Н. Касандрова, В.В. Лебедев – М.: Наука, 1970. – 195 с.
10. Светозаров, В.В. Элементарная обработка результатов измерений: учебное пособие / В.В. Светозаров. – М.: Изд. МИФИ, 1983. – 52 с.
11. Основополагающие стандарты в области метрологии. Издание официальное / М.: Изд-во стандартов, 1986 – 312 с.
ОГЛАВЛЕНИЕ
| Введение….…………………………………………………..………………….. | |
| Лабораторная работа Э-1. Изучение электростатического поля методом моделирования…………………………………………………………. | |
| Лабораторная работа Э-2. Определение электроёмкости конденсатора ….. | |
| Лабораторная работа Э-3. Определение удельного сопротивления проводника……………………………………………………………………….. | |
| Лабораторная работа Э-4. Изучение температурной зависимости сопротивления проводника и полупроводника………………………………… | |
| Лабораторная работа Э-5. Определение параметров цепи, обладающей сопротивлением и электроёмкостью……………………………………………... | |
| Лабораторная работа Э-6. Определение удельного заряда электрона методом магнетрона……………………………………………………………… | |
| Лабораторная работа Э-7. Изучение эффекта Холла в полупроводниках… | |
| Лабораторная работа Э-8. Определение характеристик петли гистерезиса ферромагнетика ………………………………………………………………… | |
| Лабораторная работа Э-9. Построение кривой намагничивания ферромагнетика методом Столетова…………………………………………… | |
| Лабораторная работа Э-10. Изучение зависимости магнитной проницаемости ферромагнетика от напряжённости магнитного поля………. | |
| Лабораторная работа Э-11. Определение точки Кюри и магнитного момента молекулы ферромагнетика …………………………………………… | |
| Лабораторная работа Э-12. Изучение электромагнитных затухающих колебаний…………………………………………………………………………. | |
| Лабораторная работа Э-13. Исследование явления резонанса в электрических цепях переменного тока………………………………………. | |
| Лабораторная работа Э-14. Изучение вынужденных электрических колебаний в контуре, содержащем катушку индуктивности с ферритовым сердечником……………………………………………………………………… | |
| Лабораторная работа Э-15. Изучение свойств сегнетоэлектриков…………. | |
| Приложение…………………………………………………………………… | |
| Библиографический список………………………………………………… |