
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Прямая засечка.
|
|
Для решения прямой засечки, заключающейся в определении координат третьего пункта по координатам двух исходных пунктов и измеренным при них углам, предложено много различных формул. Рассмотрим некоторые их них.
а) Формулы Юнга
 Рис. 2.20.
Рис. 2.20.
| Даны координаты точек А, B, C (рис. 2.20). Измерены углы β 1, β 2, β 1/, β 2/. Требуется определить координаты точки P (x, y). С выводом формул Юнга следует ознакомиться по учебнику [1, §161]. Если встать между исходными пунктами и смотреть на определяемый пункт P, то пункт А будет левым, а В – правым. |
Условимся обозначать соответствующими индексами координаты исходных пунктов и измеренные углы. Тогда формулам Юнга можно придать следующий вид:
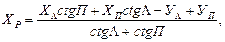 (14)
(14)
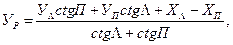 (15)
(15)
где Λ и П – значения углов при левом и правом пунктах (Λ = b 1, П = b 2).
В целях контроля находят угол γ =1800– b 1 – b 2, а затем по координатам пункта В (левый) и координатам пункта Р (правый) по формулам (14) и (15) вычисляют координаты пункта А, которые должны совпадать с заданными.
Для полного контроля полевых измерений и выписки исходных данных нужно решить, задачу, используя координаты точек В и C.
Расхождение между абсциссами и ординатами при первом и втором решении должны удовлетворять условию
 (16)
(16)
где Мr – среднее квадратическое расхождение в положении пункта Р из двух решений.
В свою очередь,
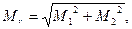 (17)
(17)
где М1 и М2 – средние квадратические ошибки положения пункта Р из первого и второго решения.
Средняя квадратические ошибки М положения пункта Р, определяемого прямой засечкой, вычисляется по формуле
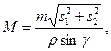 (18)
(18)
где m – средняя квадратическая ошибка измерения углов;
s1 и s2 – расстояние от исходных пунктов до определяемого (можно вычислить по координатам точек);
g – угол засечки.
Под величиной М понимается выражение
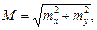 (19)
(19)
где mx и my – средние квадратические ошибки по осям координат.
Если расхождение r окажется допустимым, то за окончательное значение координат пункта Р берут среднее арифметическое, которое будет иметь ошибку
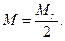 (20)
(20)
б) Формулы Гаусса.
При определении точки прямой засечкой может не быть видимости между смежными точками А, В и С. В таком случае целесообразно пользоваться формулами Гаусса, в которые входят дирекционные углы направлений с данных пунктов на определяемый (рис. 2.21).
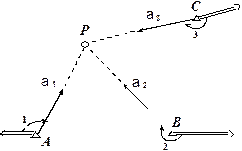 Рис. 2.21.
Рис. 2.21.
| Известны координаты точек А, B, C. Измерены углы 1, 2, 3. Требуется определить координаты точки P (X, Y). По измеренным углам и дирекционным углам направлений на другие исходные пункты, находим дирекционные углы направлений на определяемую точку α 1, α 2 и α 3. |
Запишем соответствие

откуда
 (21)
(21)
Аналогично получим
 (22)
(22)
Найдем разность

Отсюда
 (23)
(23)
Вместо (21) и (22) можно записать
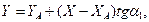 (24)
(24)
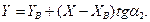 (25)
(25)
Нахождение ординат по двум формулам (24) и (25) позволяет проконтролировать вычисления. Таким образом, формулы (23), (24) и (25) – формулы Гаусса для определения координат.
Для контроля правильности полевых измерений вычисляют координаты точки Р вторично, используя другую пару исходных пунктов В и С и соответствующие дирекционные углы.