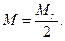Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Линейная засечка.
|
|
Задача линейной засечки заключается в определении координат третьего пункта по координатам исходных пунктов и измеренным расстояниям от определяемого пункта до исходных (однократная засечка). Для контроля определения используются координаты третьего исходного пункта и расстояния до него от определяемого.
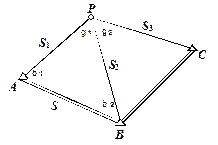 Рис. 2.24.
Рис. 2.24.
| Даны координаты пунктов А, B, C. Измерены линии S 1, S 2, S 3. Требуется определить координаты точки P (X, Y). Рассмотрим однократную засечку с использованием пунктов А и В (рис. 2.24). 1. Решением обратной геодезической задачи определим дирекционный угол и длину линии АВ: |
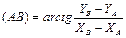 ,
,
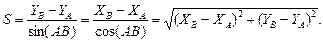
2. Определим угол β 1, используя теорему косинусов:
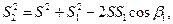 (43)
(43)
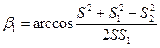 . (44)
. (44)
3. Определим дирекционный угол линии АР

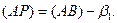 (45)
(45)
4. Определим координаты точки Р:
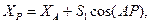 (46)
(46)
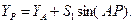 (47)
(47)
Для контроля решения задачи вычисляется длина линии ВР и сравнивается с измеренной
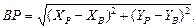 (48)
(48)
Расхождение не должно превышать 3 единиц последнего знака в измеренном значении линии S 2.
Для полного контроля определения вычисляется сторона СР и сравнивается с измеренной S 3
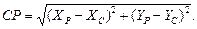 (48)
(48)
Допускается
| СР – S 3| < 6 ms, (49)
где ms – средняя квадратическая ошибка измерения расстояний S 3.
Однако в целях повышения точности окончательных значений искомых координат задачу лучше решать дважды. При втором решении используют исходные пункты В, С и расстояния S 2, S 3.
Допустимое расхождение в координатах определяют по формуле
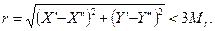
В свою очередь
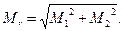
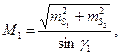
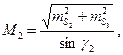 (50)
(50)
где М 1 и М 2 – средняя квадратическая ошибка положения пункта Р, определенного линейной засечкой в первом и втором вариантах;
γ – угол засечки.
Величину угла засечки (для первого решения) можно найти из выражения
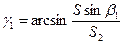 .
.
За окончательное значение координат пункта Р берут среднее арифметическое, которое будет иметь ошибку