Начальные и центральные моменты

Введенные нами числовые характеристики случайной величины: математическое ожидание, дисперсия и средне - квадратичное отклонение

являются наиболее важными. Кроме них, для описания случайных величин применяют и другие характеристики, так называемые моменты, являющиеся обобщением основных числовых характеристик.

В теории вероятностей моменты случайной величины используются для описания свойств распределения вероятностей. Наиболее употребительными являются два вида моментов: начальные и центральные.

Начальным моментом k -го порядка случайной величины X называется математическое ожидание величины X^k:

.

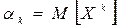Для вычисления моментов k -го порядка используются формулы:

а) в случае дискретной величины

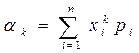
б) в случае непрерывной величины

.

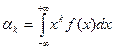Нетрудно видеть, что начальный момент первого порядка 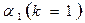есть не что иное, как математическое ожидание случайной величины X, т. е. .

Исходя из того, что начальный момент второго порядка

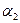=М (Х²) и D(X)=M(X²)-[M(X)]²,

можем записать

D(X) = .

Центральным моментом k -го порядка случайной величины X

называется математическое ожидание величины :

.

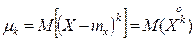Для вычисления центральных моментов k -го порядка используются формулы:

а) в случае дискретной величины

;

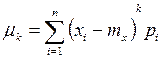б) в случае непрерывной величины

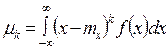
Центральный момент первого порядка есть не что иное, как математическое ожидание центрированной случайной величины 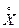, соответствующей величине X, т. е.

,

которое (как было доказано выше) всегда равно нулю: .

Центральный момент второго порядка есть дисперсия случайной величины X:

следовательно,

.

Начальные моменты главным образом служат для вычисления центральных моментов. А для чего же вводятся центральные моменты?

Центральный момент второго порядка (дисперсия), как известно, характеризует разброс (кучность) значений случайной величины около своего математического ожидания.

Кроме центрального момента второго порядка для описания случайной величины широко применяются также центральные моменты третьего и четвертого порядков.

Если распределение случайной величины симметрично относительно математического ожидания, то все центральные моменты нечетного порядка равны нулю. Этот факт следует из того, что в сумме

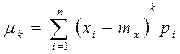
при симметричном относительно m законе распределения и нечетном k каждому положительному слагаемому будет соответствовать противоположное отрицательное слагаемое, а потому результат суммирования всегда будет равен нулю.

Аналогично в случае непрерывной величины интеграл

будет равен нулю, как интеграл в симметричных пределах от нечетной функции.

Из сказанного следует, что для характеристики асимметрии целесообразно выбрать какой-либо центральный момент нечетного порядка. Так как центральный момент первого порядка всегда равен нулю, то используют для этой цели центральный момент третьего порядка 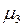, который имеет размерность куба случайной величины.

Чтобы характеристика асимметрии была отвлеченным числом, используют отношение центрального момента третьего порядка к кубу средне - квадратичного отклонения . Это отношение называется коэффициентом асимметрии или асимметрией. Коэффициент асимметрии будем обозначать через a_x.

Аналогично вводится характеристика «крутости» (острота вершины) кривой распределения. Эти свойства распределения описываются с помощью эксцесса:

.

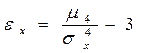Число 3 вычитается из отношения 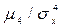потому, что для наиболее важного и распространенного закона распределения (нормального закона, с которым мы познакомимся в дальнейшем) это отношение равно 3. Следовательно, эксцесс для нормального закона равен нулю. Поэтому кривая нормального распределения является как бы эталоном, с которым сравниваются кривые других распределений.

Более островершинные кривые имеют положительный эксцесс, кривые, более плосковершинные, имеют отрицательный эксцесс.