Распределение Пуассона

Распределение Пуассона возникает в случае, когда на появление случайного события влияет много факторов, но каждый фактор в отдельности влияет слабо. Поэтому его и называют законом редких событий.

Случайные величины: поступление вызовов на телефонную станцию; число отказов элементов при испытании на надежность сложного электронного устройства; число бракованных изделий в выборках из партий, изготавливаемых заводом изделий и т. д. имеют пуассоновское распределение.

Это распределение можно рассматривать как предельный случай биномиального распределения, когда число случаев , а вероятность события в отдельном опыте стремится к нулю 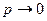. Тогда МО числа событий определится как произведение . Откуда вероятность события в одном опыте будет равна , а вероятность m событий в n опытах можно найти по формуле Бернулли

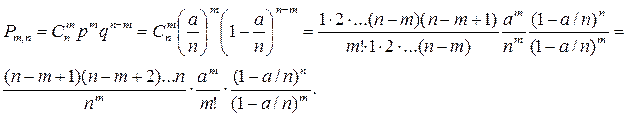
Так как число случаев , то

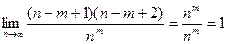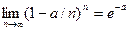, и .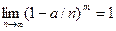

Следовательно, выражение для распределения Пуассона 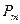(индекс n не пишут, поскольку n велико) будет иметь вид

,

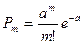где ; p - можно трактовать как МО числа появлений события в одном опыте.

В ряде практических задач величина a может определяться как:

;

;

;

,

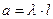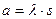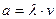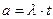где l, s, v, t – длина, площадь, объем и время соответственно;

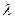- математическое ожидание числа появлений события или на участке единичной длины, или на единичной площади, или в единичном объеме, или в единичном интервале времени.

Определим математическое ожидание и дисперсию случайной величины, имеющей пуассоновское распределение. Из определения МО случайной дискретной величины следует

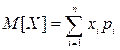, где ; .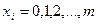

После подстановки получаем

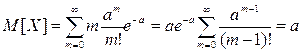. Поэтому M[X]=a.

Для нахождения дисперсии воспользуемся формулой

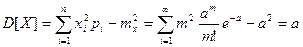. Откуда D[X]=a.

Таким образом, математическое ожидание равно дисперсии, если случайная величина имеет пуассоновское распределение.

Вероятность попадания случайной величины на заданный участок, распределенной по закону Пуассона, определяется по выражению

.
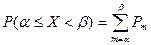