Упражнения. 2.1 Вычислите функцию распределения F(x) при x=3, если дискретная случайная величина описана рядом:

2.1 Вычислите функцию распределения F(x) при x=3, если дискретная случайная величина описана рядом:

x: 0 2 3 5

p: 0.1 0.6 0.1 0.2.

2.2 Определите вероятность попадания дискретной случайной величины в интервал a=2, b=4, если известен ее ряд распределения:

x 0 1 2 3 4 5

p 0.1 0.2 0.1 0.3 0, 05 0, 25.

2.3 Аппаратура состоит из 50 узлов. Вероятность отказа каждого узла в течение 100 часов работы одинакова и равна 0, 1. Найти математическое ожидание числа отказавших узлов за 100 часов работы.

2.4 Найдите МО дискретной случайной величины х, заданной рядом распределения:

х: -2 5 10

р: 0, 2 0, 3 0, 5.

2.5 Найдите дисперсию дискретной случайной величины X – числа отказов элементов некоторого устройства в 20 независимых опытах, если вероятность отказа элемента в каждом опыте равно 0, 3.

2.6 Дискретная случайная величина задана рядом распределения

х: 2 4 7

р: 0, 5 0, 2 0, 3.

Найдите дисперсию случайной величины.

2.6 Непрерывная случайная величина распределена равномерно в интервале (3; 9). Найдите математическое ожидание случайной величины.

2.7 Непрерывная случайная величина распределена равномерно в интервале (2; 8). Найдите дисперсию случайной величины.

2.8 Непрерывная случайная величина распределена равномерно в интервале (0; 10). Найдите вероятность попадания случайной величины в заданный интервал (3; 5).

2.9 Требуется найти вероятность попадания нормально распределенной случайной величины в интервал (5; 9), если a =5, .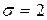

2.10 Вычислите дисперсию случайной величины T, если плотность распределения ее равна .

2.11 Случайная величина X распределена нормально с математическим ожиданием a=10. Вероятность попадания X в интервал (10; 20) равна 0.3. Чему равна вероятность попадания X в интервал (0; 10)?

2.12 Случайная величина X распределена нормально со средне квадратичным отклонением . Найти интервал, симметричный относительно математического ожидания, в который с вероятностью 0.9973 попадет случайная величина X в результате испытания.

2.13 Найдите дисперсию показательного распределения, заданного плотностью вероятности .

2.14 Найдите средне квадратичное отклонение случайной величины от центра группирования показательного распределения, заданного функцией распределения 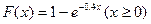.