Расчет моды и медианы в интервальном ряду распределения

Модальное значение признака (Мо) рассчитывается по формуле:

,

где 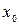-нижняя граница модального интервала; i - шаг интервала;

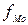-частота модального интервала; -частота интервала, предшествующего модальному; 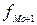-частота интервала, следующего за модальным.

Для ряда с неравными интервалами, расчет моды производится

по следующей формуле: ,

где m - плотность распределения в соответствующем интервале.

Плотность распределения, это число случаев, приходящихся на единицу интервала.

m= f/i (абсолютная плотность распределения);

m = 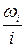(относительная плотность распределения). I

Расчет медианы производится по формуле:

,

где 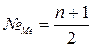- номер медианы;

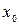- нижняя граница медианного интервала;

i-шаг интервала; 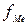- частота медианного интервала.

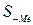- накопленные частоты, предшествующие медианному интервалу;

Пример. Рассчитать моду и медиану, по ниже представленным данным, о размере платежей за жилищно- коммунальные услуги (в руб.) в расчете на 1чел.(18кв. м.) по 55районам одного из регионов РФ:

Размер платежей, руб. Х.	Число районов, f	Накопленные частоты, S
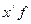
155-160			157, 5	472, 5
160-165			162, 5	1625, 0
165-170			167, 5	3350, 0
170-175			172, 5	3795, 0
Итого				9242, 5

; ;

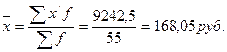
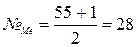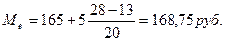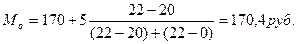
Рассчитаем моду для ряда с неравными интервалами, используя: а) абсолютную плотность распределения; б) относительную плотность распределения.

Пример. Ниже представлено распределение вкладчиков по размерам вклада в одном из сбербанков района:

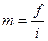
Размер вклада, руб.- х	Число вкладчиков, f	Частость,	Абсолютная плотность распределения,	Относительная плотность распределения,
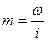
500-1500
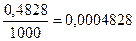
1500-5000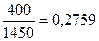
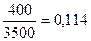
5000-7500
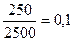
Свыше- 7500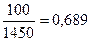
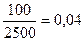
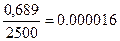
Итого		1, 0

а) = = ;

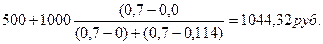б)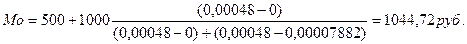

Расхождение в результатах объясняется округлениями, допущенными в ходе расчетов в варианте «б».