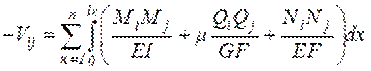Теорема о взаимности работ

Небольшое перемещение, которое позволяют связи данной системы, называется возможным перемещением.

Вызывать данное перемещение могут какие-либо силы, изменение температуры, осадка опор и др.

Работа силы на возможном перемещении называется возможной работой.

Возможное перемещение обозначим Δ _ij, а возможную работу А_ij (здесь i означает направление, а j – причину).

Пример: если какой-либо точке балки вначале действует сила P_i, а через некоторый промежуток времени в другой точке на балку начнет действовать другая сила P_j, то балка в точке действия силы P_i получит возможное перемещение Δ _ij (рис. 1, а). Поскольку в это время величина силы P_i остается постоянной, совершаемая ею возможная работа определяется площадью прямоугольника (рис. 1, б):

А_ij=P_i Δ _ij

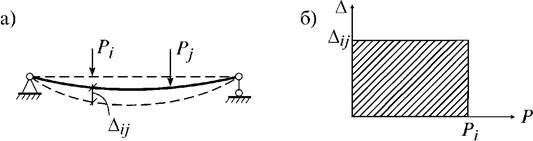
Рисунок 1. Возможное перемещение

Таким образом, возможная работа равна произведению силы на возможное перемещение.

При определении возможной работы необходимо рассматривать два состояния системы: в первом из них действуют заданные, а во втором – возможные силы.

Теорема Бетти (теорема о взаимности работ): возможная работа сил i-го состояния на перемещениях j-го состояния равна возможной работе сил j-го состояния на перемещениях i-го состояния.

P_i Δ _ij=P_j Δ _ji

Пусть на систему воздействуют силы P₁ и P₂. Приложим их в разной последовательности и рассмотрим два состояния системы:

1) прикладывается сила P₁, затем сила P₂ (рис. 2, а);

2) прикладывается сила P₂, затем сила P₁ (рис. 2, б).

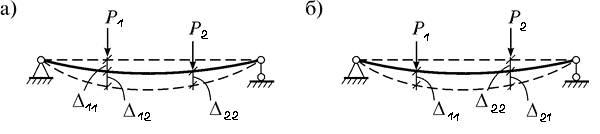
Рисунок 2. Возможное перемещение

P₁ Δ ₁₂=P₂ Δ ₂₁

Теперь определим возможную работу внутренних сил. Для этого рассмотрим два состояния системы:

1) действует сила P_i, которая вызывает внутренние усилия M_i, Q_i, N_i;

2) действует сила P_j, которая в пределах малого элемента dx вызывает возможные перемещения.

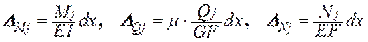
Внутренние усилия первого состояния на возможных перемещениях второго состояния совершат возможную работу:

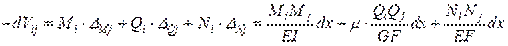
Если взять определенный интеграл для указанного выше выражения по длине элемента l и учесть наличие в системе n стержней, получим формулу возможной работы внутренних сил: