
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет разветвленных цепей переменного тока символическим методом
|
|
Пример. Найти токи в схеме (рис. 3.15). Положительные направления ЭДС указаны на схеме стрелками,
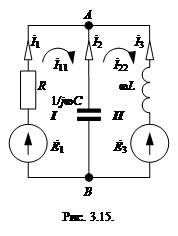
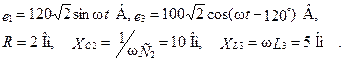
Решение. Запишем ЭДС в комплексной форме:  Выберем положительные направления для токов в ветвях к узлу А.
Выберем положительные направления для токов в ветвях к узлу А.
1. Проведем расчет цепи методом двух узлов Определим проводимости ветвей: Y 1=1/ Z 1=1/2=0, 5 См; Y 2=1/ Z 2=l/(– j 10)= j 0, 1 См; Y 3=1/ Z 3=1/(j 5)=– j 0, 2 Cm. Заземлим точку B. Составим уравнение для расчета межузлового напряжения: 
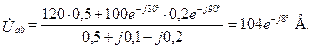
Токи ветвей найдем по закону Ома для участка цепи, содержащего источник ЭДС:

2. Проведем расчет цепи методом контурных токов.
Собственные сопротивления контуров I и II:
Z 1= R 1– jXC 2=2– j 10 Ом, Z 2= j (XL3 – XC 2)=– j 5 Ом.
Общее сопротивление контуров I и II: Z 12= Z 21=– jXC 2=– j 10 Ом.
Составим систему уравнений:
İ 11 Z 1– İ 22 Z 12= Ė 1
-İ 11 Z 12+ İ 22 Z 2=– Ė 3
İ 11(2– j 10)– İ 22(– j 10)=120
– İ 11(– j 10)+ İ 22(– j 5)=–100 е –30°=–(86, 6– j 50)
Решая систему относительно тока İ 11, получим:
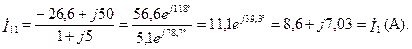
Подставим полученное значение тока İ 11 во второе уравнение системы:
j 10(8, 6+ j 7, 03) –j 5 İ 22= – 86, 6+ j 50; j 5 İ 22= – 16, 3 –j 36; İ 22=7, 2 –j 3, 26=7, 9 e–j 24, 3°;
İ 3= –İ 22=7, 9 ej (180–24, 3°)=7, 9 ej 155, 7° (A);
İ 2= İ 22 –İ 11=7, 2 –j 3, 26–8, 6– j 7, 03=–1, 4– j 10, 3 = 10, 4 e–j 98° (A).
Оба способа решения задачи дают практически одинаковые результаты. Небольшие расхождения объясняются неточностью при вычислении значений тригонометрических функций при углах, близких к 0 или ±90°.