Резонанс токов.

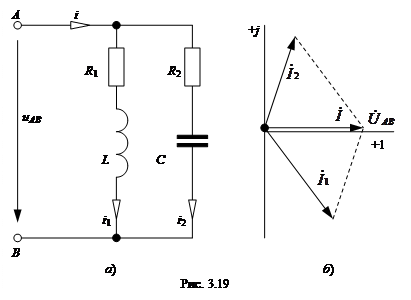
Резонанс токов наблюдается при параллельном соединении ветвей, в одной из которой находится индуктивный элемент, а в другой – емкостный элемент (рис. 3.19).

Пусть на вход цепи подается синусоидальное напряжение и_AB = U_m sin(ω t +ψ _u) , под действием которого будет протекать синусоидальный ток: i = I_m sin(ω t +ψ _i) .

Связь между током и напряжением определяется по закону Ома: .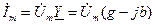

Резонанс токов возникает, когда φ =ψ _u –ψ _i =0, что имеет место при равенстве нулю реактивной проводимости b. Запишем комплексные проводимости ветвей:

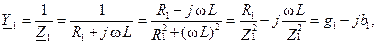
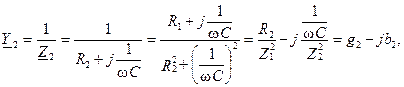
Ток в первой ветви отстает от напряжения и может быть записан как .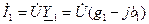

Ток во второй ветви опережает напряжение и может быть записан как .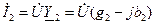

Ток в неразветвленной части цепи .

По определению резонансного режима ток 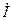должен совпадать по фазе с напряжением 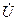. Это будет при условии, что сумма реактивных проводимостей ветвей равна нулю: b ₁+ b ₂=0.

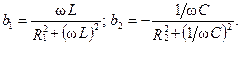
Следовательно, условие наступления резонанса токов можно записать так:

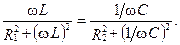
На рис. изображена векторная диаграмма для резонансного режима. В частном случае, если R ₂=0, то резонанс наступит при

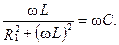
В еще более частном случае, при выполнении условия R ₁< < ω L резонанс наступит при 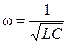(сравните с резонансом напряжений).

В общем случае резонанса токов можно достичь путем изменения величин ω, R ₁, R ₂, L, С. Значение тока I в неразветвленной части цепи может быть меньше токов каждой из ветвей. При R ₂=0, R ₁≈ 0 ток I может оказаться ничтожно малым по сравнению с токами I ₁ и I ₂. В идеализированном случае, когда, R ₁= R ₂=0, ток в неразветвленной части равен нулю и входное сопротивление цепи равно бесконечности.

Определим резонансную частоту из условия b ₁+ b ₂=0:

.

Добротность параллельного контура определяется выражением .

Эквивалентное сопротивление параллельного контура при условии R ₂=0 при резонансе может быть вычислено по формуле

.
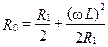