Гармонические колебания и их характеристики

Колебания, при которых колеблющаяся величина 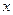изменяется со временем по закону синуса или косинуса, называется гармоническими.

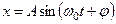или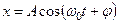

Здесь – амплитуда величины , наибольшее отклонение от положения равновесия; 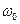- циклическая частота; 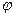- начальная фаза; 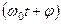– фаза, определяет значение 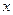в момент времени .

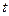Колебания характеризуются частотой 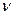и периодом .

– время одного полного колебания

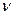– число полных колебаний за единицу времени.

Приведенные выше выражения для 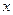являются решением дифференциального уравнения (дифференциальное уравнение гармонических колебаний)

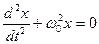
На рис.9 дан график гармонических колебаний:

рис.9

Кинетическая энергия материальной точки, совершающей прямолинейные гармонические колебания, равна

Потенциальная энергия материальной точки, совершающей гармонические колебания под действием силы упругости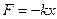

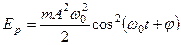
Полная энергия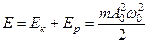

Пружинный маятник –это груз массой m, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием силы упругости 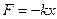(k – жесткость пружины).

Дифференциальное уравнение колебаний пружины, полученное на основе второго закона Ньютона, имеет вид

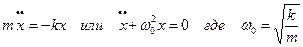
Решение этого уравнения: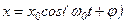

Период колебаний пружинного маятника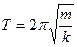

Формула для периода справедлива в случае, когда масса пружины мала по сравнению с массой груза.

Физический маятник – твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси О, не проходящей через центр масс тела С (рис.10).

Малые колебания физического маятника описываются дифференциальным уравнением

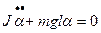или

рис.10

где 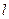– расстояние ОС, 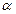– угол отклонения маятника.

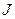– момент инерции тела относительно оси, проходящей через

точку О.

Решение этого уравнения имеет вид:

,

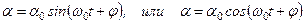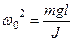
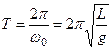
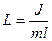– приведенная длина маятника

Точка на продолжении прямой ОС, отстоящая от точки подвеса маятника на расстоянии приведенной длины, называется центром качения физического маятника. Точки О и взаимозаменяемы.

Математический маятник – материальная точка массой , подвешенная на нерастяжимой невесомой нити, колеблющаяся под действием силы тяжести.

Практически приближением такой идеализованной системы являются небольшой тяжелый шарик, подвешенный на тонкой нити длиной .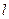

Период малых колебаний математического маятника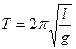

Приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника.

Затухающие колебания – колебания с уменьшающейся амплитудой (рис.11).

рис.11

Амплитуда уменьшается из-за совершения работы по преодолению сил трения среды.

Если сила трения (сила сопротивления) пропорциональна скорости тела,

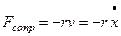где – коэффициент трения,

то дифференциальное уравнение затухающих колебаний имеет вид:

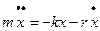или

Решение уравнения:

Амплитуда затухающих колебаний – .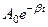

Коэффициент затухания 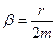, циклическая частота колебаний при этом

Характеристики затухающих колебаний – декремент затухания, логарифмический декремент затухания, коэффициент затухания.

Декремент затухания показывает во сколько раз амплитуда колебаний уменьшается за один период Т, т.е.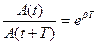

Натуральный логарифм декремента называется логарифмическим декрементом затухания

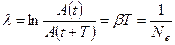
– число колебаний, за которое амплитуда уменьшается в е раз.

Коэффициент затухания 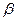– величина, обратная промежутку времени, за которое амплитуда уменьшается в е раз.

Добротность колебательной системы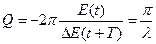

Добротность определяется отношением энергии колебательной системы, которую она имеет в момент времени 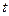, к убыли энергии за период. Чем выше добротность колебательной системы, тем медленнее затухают колебания.

Вынужденные колебания – колебания, возникающие под действием внешней периодически изменяющейся силы.

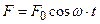
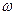– частота колебаний вынуждающей силы.

Дифференциальное уравнение вынужденных колебаний

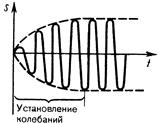
рис.12

На рис.12 изображен график вынужденных колебаний. Амплитуда вынужденных колебаний зависит от частоты вынуждающей силы.

При некотором значении 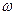, близком к собственной частоте колеблющейся системы , амплитуда резко возрастает, т.е. наблюдается резонанс. Кривая зависимости амплитуды от частоты вынужденных колебаний 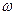называется резонансной кривой

(см. рис.13).

рис.13

Волны

1. Волновые процессы. Процесс распространения колебаний в упругой среде называется волновым процессом (волной).

Если колеблющееся тело (камертон, струна, мембрана и т.д.), находится в упругой среде, то оно приводит в колебательное движение соприкасающиеся с ним частицы среды, вследствие чего в прилегающих к этому телу элементах среды возникают периодические деформации (например, сжатия и растяжения). При этих деформациях в среде появляются упругие силы, стремящиеся вернуть элементы среды в исходное состояние. Упругие деформации будут передаваться от одних участков среды к другим, более удаленным от источника колебаний.

Таким образом, периодические деформации, вызванные в каком-нибудь месте упругой среды, будут распространяться в среде с некоторой скоростью. При этом частицы среды, совершают колебательные движения около положений равновесия;

от одних участков к другим передается лишь состояние деформации.

Основным свойством волн является перенос энергии без переноса вещества.

Упругие волны бывают продольными и поперечными. В продольных волнах частицы среды колеблются в направлении распространения волны, в поперечных – в плоскостях, перпендикулярных направлению распространения волны. В жидкостях и газах возникают только продольные волны, а в твердом теле – как продольные, так и поперечные.

Синусоидальные (гармонические) волны. Упругая волна называется гармонической, если соответствующие ей колебания частиц среды являются гармоническими. На рис.14 приведен график гармонической волны в момент времени t.

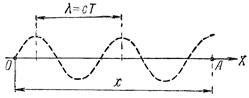
рис.14

Этот график дает зависимость смещения всех частиц среды от расстояния до колеблющегося тела и времени.

Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны 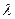. Ее можно определить по формуле

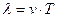
– период колебаний; 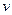– скорость волны.

Волновая поверхность – геометрическое место точек, колеблющихся в одинаковой фазе.

Фаза волны – геометрическое место точек, до которых доходят колебания к моменту времени t (одна из волновых поверхностей).

Фазовая скорость – это скорость распространения волнового процесса.

Волновые поверхности могут быть любой формы. В простейшем случае они представляют совокупность плоскостей, параллельных друг другу, или совокупность концентрических сфер. Соответственно волна называется плоской или сферической.

Уравнение волны. Распространение волн в однородной изотропной среде описывается дифференциальным уравнением в частных производных

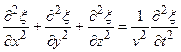
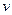– скорость распространения волны (фазовая скорость);

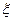– определяет смещение частицы среды от положения равновесия.

Частным решение этого уравнения является функция

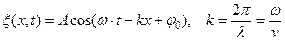– волновое число.

Эта функция описывает бегущую гармоническую волну.