Модель Асинхронного двигателя во вращающейся системе координат в MATLAB

При выполнении курсовой работы, связанных с моделированием асинхронного двигателя, возникает необходимость увеличения вариантов их модификаций. Одним из способов решения этой задачи является возможность выразить электромагнитный момент через различную комбинацию переменных токов и потокосцеплений двигателя [1, c.238] и [2]. Основные уравнения математической модели АД, записаны в векторной форме в относительных единицах, имеют следующий вид [3]:

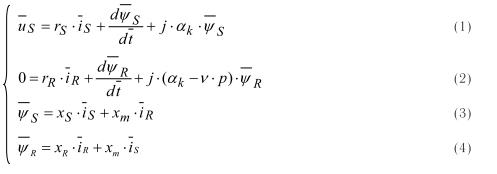
рассмотрим асинхронный двигатель с коротко замкнутым ротором , кроме того, определим электромагнитный момент по следующей формуле [1, с.238]

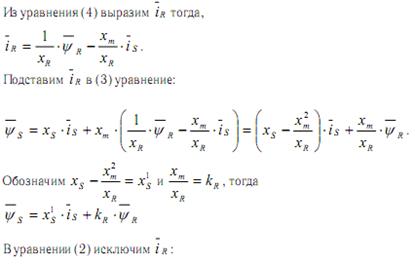
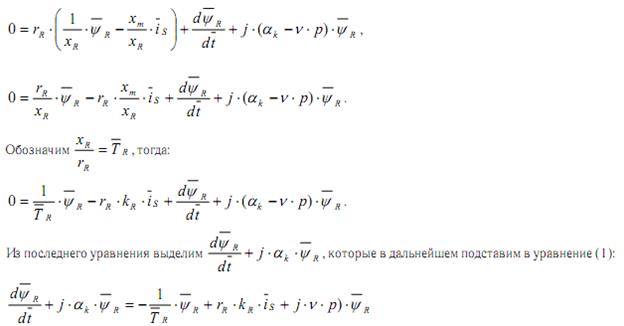
В уравнений (1) сделаем следующие преобразования:

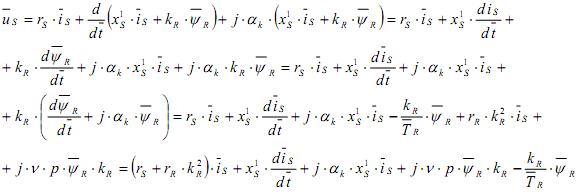
Обозначим r_S+r_R+k_r²=r тогда:

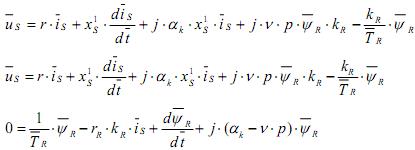
Вещественную ось обозначим α, а мнимую через δ. Пространственные векторы в этом случае раскладываются по осям:

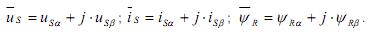
Подставим эти значения в уравнения и, приравняв отдельно вещественные и мнимые части, получим:

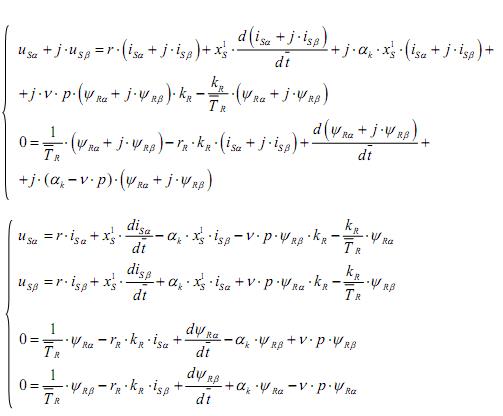
С учетом электромагнитных моментов система уравнений в операторной форме 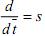примет вид:

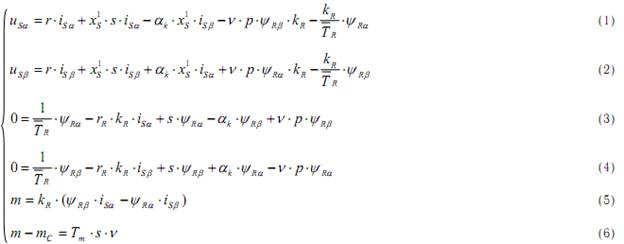
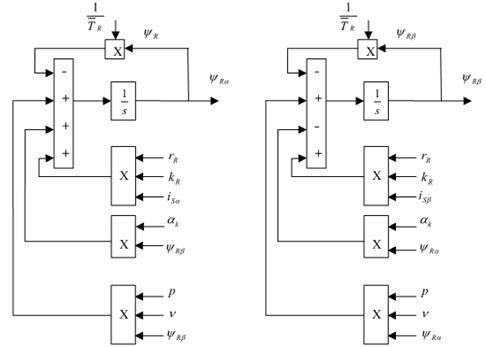
Структурная схема для уравнений (1) и (2):

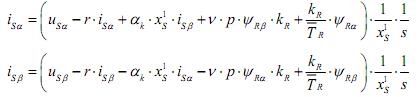
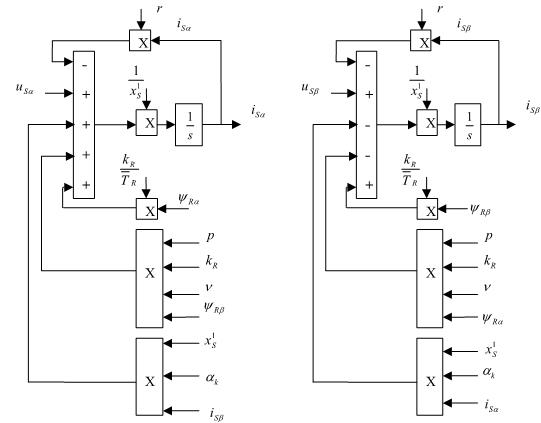
Структурная схема для уравнений (3) и (4):

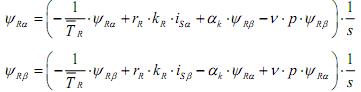
рассмотрим трехфазный асинхронный короткозамкнутый двигатель со следующими номинальными данными и пар

метрами схемы замещения [4].

Номинальные данные:

номинальная мощность............................................... P = 38 кВт

номинальное фазное напряжение...................................... U1 = 220 B

номинальный фазный ток............................................. I1 = 192 A

номинальная частота................................................. f = 50 Гц

номинальная синхронная скорость.....................................𝛺 0N =104.7 рад/с

номинальная скорость ротора......................................... 𝛺 N =38.223рад/с

номинальный КПД...................................................nN = 0.95

номинальный коэффициент мощности............................ cos 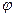N = 0.92

число пар полюсов.............................................p = 2

Параметры Т-образной схемы замещения при номинальной частоте

Активное сопротивление обмотки статора........................ RS = 0.083 Ом

индуктивное сопротивление рассеянья обмотки статора.............L_sδ = 0.008Ом

активное сопротивление обмотки ротора, приведенное к статору.......Rr = 0.041 Ом

индуктивное сопротивление рассеянья обмотки ротора,..............Lrб = 0.0012 Ом

главное индуктивное сопротивление..............................Xm =0.0318 Ом

Суммарный момент инерции двигателя и механизма.................J = 0.45 кг∙ м2

Базисные величины системы относительных единиц.

Напряжение, В.....................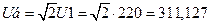

Ток, А.....................................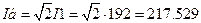

Частота а, рад /с........................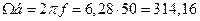

Скорость ротора, рад /с...........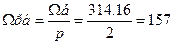

Сопротивление, О м................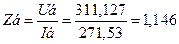

Потокосцепление, В *с..............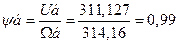

Индуктивность, Гн.................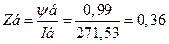

В качестве базисного значения моментов двигателя и статического механизма выбираем значение электромагнитого момента двигателя в номинальном режиме:

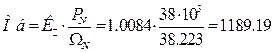
где 1.0084 kD =1.0084 – коэффициент, учитывающий различие значений электромагнитного момента и момента на валу двигателя в номинальном режиме.

В качестве базисной мощности выбираем значение электромагнитной мощности двигателя в номинальном режиме, определяемое по следующей формуле: Вт

Относительные значения параметров схемы замещения двигателя.

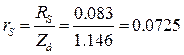
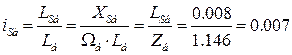
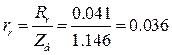
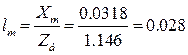
Механическая постоянная времени системы «двигатель-механизм» составляет:

Модель АКЗ, построенная по уравнениям (1) – (6), представлена на рис. 37-41. На вход модели в момент времени t=0 подаются напряжения 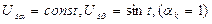, тем самым реализуя прямой пуск.

Осциллоскопы измеряют относительные значения электромагнитного момента и скорости. результаты моделирования представлены на рис. 2. Они показывают, что при прямом пуске вначале наблюдается значительные колебания момента. Такие же колебания наблюдаются в токе и скорости.

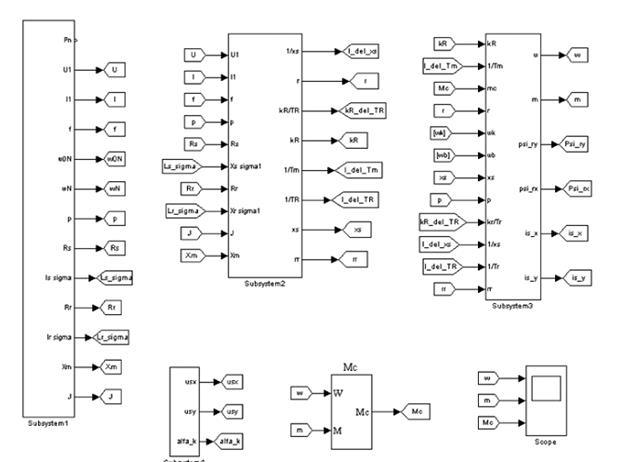
Рис. 66. Полная модель АКЗ во вращающейся системе координат с переменными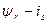

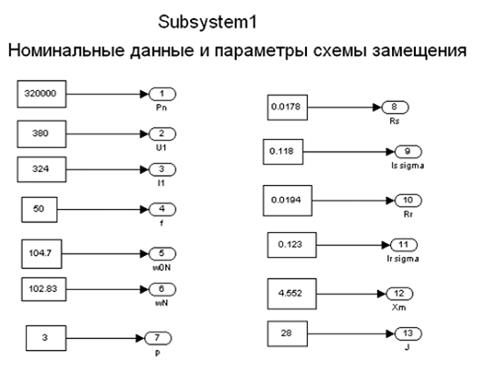
Рис. 67.Номинальные данные и параметры схемы замещения

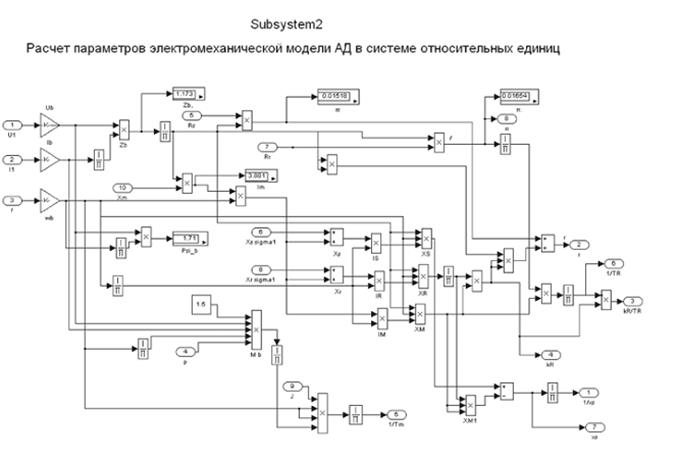
Рис. 68.Расчет параметров модели АД в системе относительных едениц

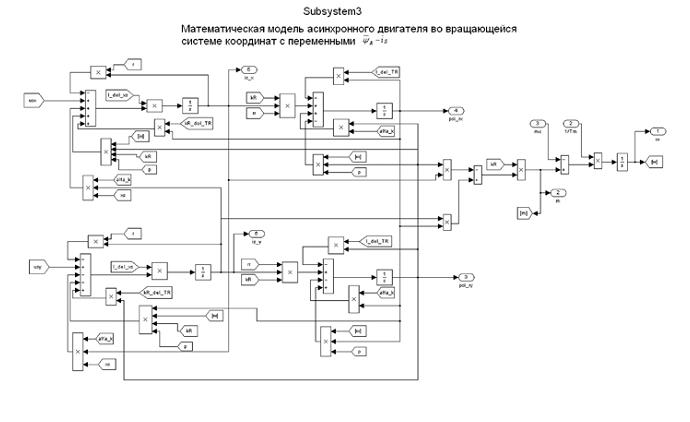
Рис. 69.Математическая модель АД во вращающейся системе координат

Рис. 70.Преобразователь координат

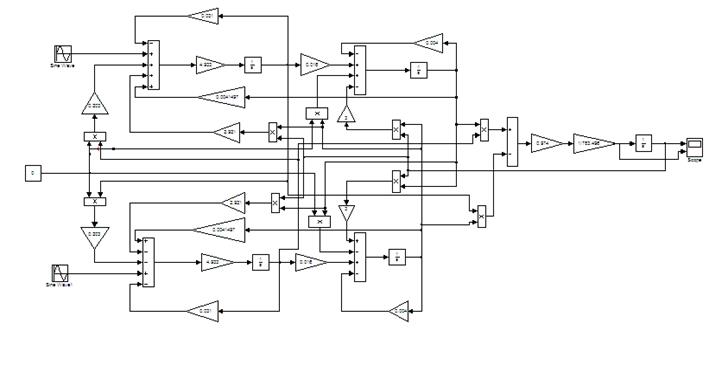
Рис. 71. Математическая модель АД во вращающейся системе координат без SubSystems

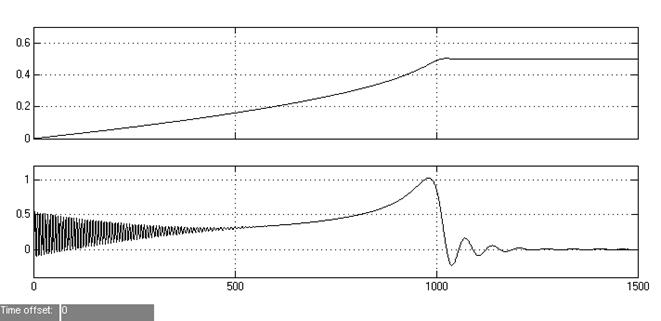
Рис. 72.График прямого пуска АД во вращающейся системе координат