Расчет статически неопределимой рамы методом перемещений

З а д а н и е. Для заданного статически неопределимой рамы (рис. 7) с выбранными по шифру из табл.7 размерами и нагрузкой требуется построить эпюры изгибающих моментов, поперечных и продольных сил.

Таблица 7

Первая цифра шифра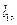

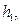(м)

(м)

Вторая цифра шифра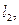

(м)

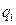
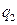
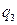
Последняя цифра шифра и номер схемы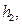

(м)

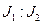
кН/м

1: 2

2: 1

2: 3

3: 2

1: 3

3: 1

3: 4

4: 3

4: 1

1: 4

У к а з а н и я к р е ш е н и ю з а д а ч и. При выборе основ­ной системы метода перемещения необходимо учитывать, что линейные связи должны быть поставлены не только по направлению возможных ли­нейных перемещений_, но и для устранения мгновенной изменяемости системы, образованной после постановки шарниров во всеузлы (включая жесткие опоры).

При построении единичных и грузовых эпюр моментов используются таблицы реакций, имеющиеся в учебниках.

Прежде чем приступить к подсчету коэффициентов канонических урав­нений, необходимо значения ординат на всех единичных эпюрах выразить через какую-либо одну жесткость (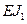 или 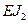). Удобно также перейти к погонным жесткостям стержней ().

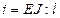Коэффициенты и свободные члены канонических уравнений можно легко определить по единичным и грузовой эпюрам.

Дальнейший расчет (решение системы канонических уравнений, пост­роение эпюр от найденных значений неизвестных и окончательной эпюры) производится аналогично методу сил.

Решение данной задачи рекомендуется проводить с использованием ЭВМ. В этом случае коэффициенты канонических уравнений следует опре­делять аналогично методу сил (" перемножением" эпюр):

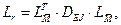
где 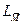- матрица значений моментов от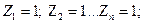

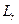- матрица значений коэффициентов канонических уравнений.

Вектор свободных членов

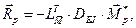
где 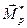- вектор моментов из эпюры, построенной от нагрузки в любой основной системе метода сил.

Далее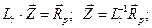

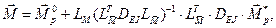
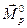- вектор моментов их эпюры 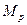, построенный в основной системе метода перемещений.

Здесь, как и в указаниях к задаче № 4, формирование матрицы жест­кости и векторов, входящих в матрицу 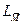, надо производить с уче­том ординат эпюры .

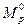Эпюры Qи Nстроятся по эпюре 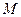(см. указания к задаче №4).

Проверку полученных эпюр надо проводить как статическую (равнове­сие узлов и рамы в целом), так и кинематическую. Для последней про­верки необходимо построить хотя бы одну единичную эпюру в основной системе метода сил и " умножить" ее на окончательную эпюру М по правилу Верещагина.

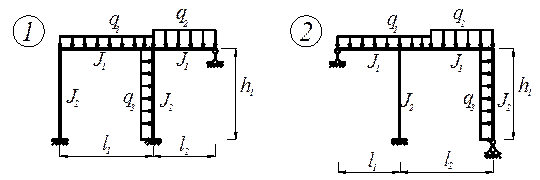
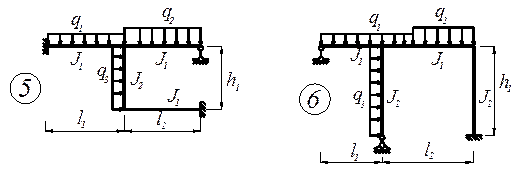
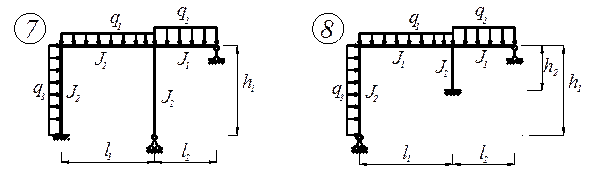
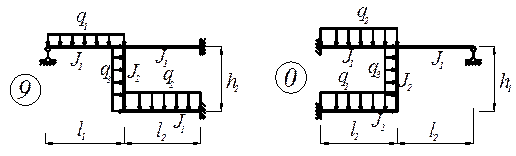
Рис. 9

Литература

1. Дарков А.В., Шапошников Н.Н. Строительная механика. – М.: Высшая школа, 1986.

2. Строительная механика./ Под ред. А.В. Даркова. – М.: Высшая школа, 1976.

3. Снитко Н.К. Строительная механика. – М.: Высшая школа, 1978.

4. Дыховичный А.И. Строительная механика. – М.: Высшая школа, 1966.

5. Руководство к практическим занятиям по курсу строительной механики. / Под ред. Г.К. Клейна. – М.: Высшая школа, 1973.

6. Киселев А.В., Афанасьев А.М., Ермоленко В.А. и др. Строительная механика в примерах и задачах. – М.: Стройиздат, 1968.

7. Анохин Н.Н. Строительная механика в примерах и задачах. Ч.1. Статически определимые системы. Учеб пособие. – М: Изд-во АСВ, 1999 – 335с.

8. Строительная механика. Основы теории с примерами расчётов. Учебник под ред. А.Е. Саргсяна – М.: Изд-во АСВ, 1998 – 320. с илл.

9. Иванов Е.Г., Ворожейкин С.Е. Строительная механика: Статика сооружений: Учебное пособие. Чебоксары: Изд-во Чуваш. ун-та, 2001. 228 с.