Примеры метрических пространств

Пример 1.1. Пусть R – множества действительных чисел. Для любых чисел x, yÎ R введем функцию r (x, y) = ½ х- в ½ (1.1). Очевидно, что (1.1) удовлетворяет аксиомам 1 и 2 метрики. Покажем, что функция r удовлетворяет аксиоме 3

" x, y, zÎ R:

r (x, y) = ½ х - в ½ = ½ х- z + z- в ½ £ ½ х - z ½ + ½ z - в ½ = r (x, z) + r (z, y).

Пара (R, r), где r определено равенством (1.1) – метрическое пространство. Его обозначают R или R ¹.

Пример 1.2. Множества М= [ a, b ] с метрикой r (x, y) = ½ х- в ½ " x, yÎ [ a, b ]обозначают Х = ([ a, b ], r). Х – подпространство метрического пространства R, поскольку [ a, b ] Ì R .

Пример 1.3. Множества рациональных чисел Q с метрикой, которая определена формулой (1.1) для всех x, y Î Q, является метрическом пространством. Пространство Х = (Q, r) – подпространство метрического пространства R и обозначается через Q.

Пример 1.4. Обозначим через R ^m множества упорядоченных совокупностей m действительных чисел . Элементы множества R ^m называются векторами (точками) и обозначаются одной буквой х = (х₁, х₂, …, х_m), y = (y₁, y₂ , …, y_m). Числа х₁, х₂ , …, х_m – координаты вектора х. Элементы х и в равны между собой, т.е. х = в, тогда и только тогда, когда х ₁ = у ₁, х ₂ = у ₂, …, х_m = у_m.

На множестве R ^m введем функцию r (x, y):

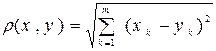" x, yÎ R ^m. (1.2)

Покажем, что пространство (R^m , r) = R ^m, где r определено равенством (1.2), является метрическом пространством.

Функция r удовлетворяет первым двум аксиомам метрики. Для того, чтобы показать, что функция удовлетворяет аксиоме 3, докажем две леммы.

Лемма 1.1. Для любых действительных чисел a_k, b_k, k= 1, 2, …, m, имеет место неравенство Коши-Буняковского:

(1.3)

3Рассмотрим функцию

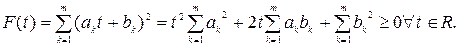
Поскольку квадратный трехчлен неотрицательный, то дискриминант неположительный:

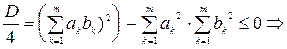
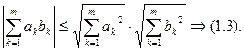4

Лемма 1.2. Для любых действительных чисел a_k, b_k, где k = 1, 2, …, m имеет место неравенство Минковского:

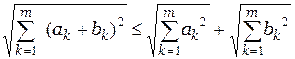. (1.4)

3

Þ 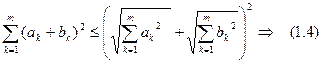.4

Покажем, что для функции (1.2) выполняется аксиома 3 для любых трех точек х = (х₁, х₂, …, х_m), y = (y₁, y₂ , …, y_m), z = (z₁, z₂, …, z_m). Обозначим

a_k = x_k – z_k, b_k = z_k – y_k Þ a_k + b_k = x_k – z_k + z_k – y_k= x_k – y_k. (1.5)

Подставим в неравенство (1.4) значения из (1.5) и получим

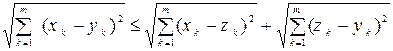Þ

Þ r (x, y) £ r (x, z) + r (z, y). 4

Пример 1.5. Рассмотрим также множества R ^m , но r зададим с помощью формулы

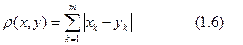
где х = (х ₁, х ₂, …, х_m), y = (y ₁, y ₂, …, y_m) – произвольные точки (векторы) пространства R ^m. Докажем, что функция (1.6) удовлетворяет аксиомам метрики.

Функция r удовлетворяет первым двум аксиомам метрики. Покажем, что r удовлетворяет аксиоме 3 для любых трех точек

х = (х ₁, х ₂, …, х_m), y = (y ₁, y ₂, …, y_m), z = (z ₁, z ₂, …, z_m)пространства R^m.

3

Þ r (x, y) £ r (x, z) + r (z, y). 4

Пример 1.6. Рассмотрим множества С [ a, b ] всех действительных функций, непрерывных на [ a, b ]. Для любых двух функций x (t) и y (t) из этого множества положим

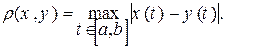(1.7)

Равенство (1.7) – чебышовское расстояние между функциями x (t) и в (t). Покажем, что функция r (x, y)– метрика на множестве С [ a, b ].

Функция r удовлетворяет первым двум аксиомам метрики. Покажем, что r удовлетворяет аксиоме 3.

3Пусть x, y, z Î С [ a, b ]. Тогда t Î [ a, b ]. Оценим разность

½ x (t) - y (t)½ = ½ x (t) - z (t) + z (t) - y (t)½ £ ½ x (t) - z (t)½ + ½ z (t) - y (t)½ £

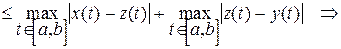
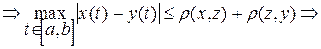r (x, y) £ r (x, z) + r (z, y). 4

Пример 1.7. Рассмотрим l₂ – множества различных числовых последовательностей х ₁, х ₂ ,..., х_n … действительных чисел, для которых сходится ряд 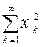. Для любых двух элементов х = х ₁, х ₂ ,... и в = у ₁, у ₂... этого множества определим

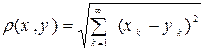. (1.9)

Т.к. ряд 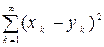сходится, то формула (1.9) определяет функцию для любых х, вÎ l ₂. Сходимость этого ряда легко доказать с помощью признака сравнения рядов, если учесть сходимость рядов 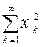и 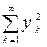и очевидное неравенство .

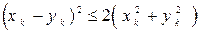Функция r, заданная формулой (1.9), удовлетворяет аксиомам 1 и 2 (Очевидно). Докажем, что она удовлетворяет и аксиоме 3.

3Для любых трех элементов x, y, z множества l ₂ имеет место неравенство

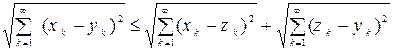Þ r (x, y) £ r (x, z) + r (z, y). 4