Последовательности точек метрического пространства

Определение 4.1. Последовательностью точек метрического пространства (Х, r)называется отображение f множества натуральных чисел в множество Х: f: N X.

Значение этого отображения в точке n Î N называется n -м элементом последовательности точек метрического пространства и обозначается: x_n = f (n), последовательность(x_n)или последовательность (х₁, х₂, …, х_n…) или(х_n = (х₁, х₂, …, х_n, …)).

Пример 4.1. В пространстве R²: , где х₁= (1; 2), х₂= (1/2; 3/2).

Пример 4.2. В пространстве С [a, b]: 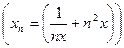, где х₁ = 1 /x + x,

х₂ = 1/2 x + 4 x, … " xÎ [2, 3].

Определение 4.2. Пусть (x_n)– последовательность точек метрического пространства (Х, r), (k₁, k₂, …, k_n, …) – возрастающая последовательность натуральных чисел. Тогда последовательность 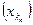называется подпоследовательностью последовательности (x_n).

Пример 4.3. Последовательность – подпоследовательность последовательности .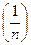

Определение 4.4. Пусть (x_n)– последовательность точек метрического пространства (Х, r). Точка а Î Х называется пределом последовательности (x_n) если:

(" e > 0)($ N (e))(" n> N) Þ [ r (x_n, a)< e ]

Это оределение можно сформулировать иначе: точка а Î Х называетсяпределом последовательности (x_n), если r (x_n, a)® 0, при n ®¥.

Обозначается

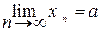
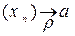по метрике r или , если n®¥.

Если последовательность (x_n) имеет предел, то она называется сходящейся, в противном случае – расходящейся.

Если (x_n) – последовательность метрического пространства (Х, r) сходится к числу аÎ Х, то а – предельная точка последовательности (x_n).

Обратное, вообще говоря, не имеет место.

Для сходящихся последовательностей имеют место следующие теоремы.

Теорема 4.1. Если (x_n) – сходящаяся последовательность метрического пространства (Х, r), то ее предел единственен.

3Пусть

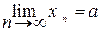Û r (x_n, a) ® 0 и 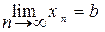Û r (x_n, b) ® 0.

По аксиомам метрики 0 £ r (a, b) £ r (x_n, a) + r (x_n, b). Перейдем к пределу, если n®¥, получим r (a, b) = 0 Û a=b. 4

Теорема 4.2. Если (x_n) – сходящаяся последовательность метрического пространства (Х, r), то она ограниченная.

3Пусть .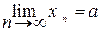

По определению предела последовательности для любого e> 0, в частности для e=1, существует такой номер N, что для всех n> N выполняется неравенство r (a, x_n) < 1.

Положим число r = max {1, r (x₁, a), r (x₂, a), …, r (x_N, a)}. Очевидно, что

r (x_n, a) £ r " nÎ N. Можно сделать вывод, что все элементы данной последовательности находятся в шаре с центром в точке а и радиусом r. А это значит, что данная последовательность ограниченная. 4

Теорема 4.3. Если последовательность (x_n) метрического пространства (Х, r)сходится к числу а Î Х, то любая ее подпоследовательность сходится к а.

3Пусть 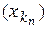– произвольная подпоследовательность последовательности(x_n). По условию 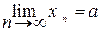.Это означает следующеее: (" e> 0)($N (e))(" n> N)Þ [ r (x_n, а) < e ].

Поскольку k_n ³ n, то для всех n> N будем иметь k_n > N и поэтому r .

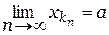Таким образом мы доказали, что (" e> 0)($N(e))(" n> N) Þ [ r ]. Это значит, что . 4