
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства сходящихся последовательностей в некоторых метрических пространствах
|
|
Теорема 5.1 (о покоординатной сходимости последовательности в метрическом пространства Rm). Для того, чтобы последовательность точек метрического пространства Rm (хn = (х1(n), х2(n), …, хm(n), …)) сходилась к точке а = (а1, а2, …, аm) этого пространства, необходимо и достаточно, чтобы числовые последовательности (х1(n)), (х2(n)), …, (хm(n)) сходились соответственно к числам а1, а2, …, аm:
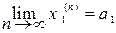 ,
, 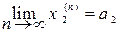 ,...,
,...,  (5.1)
(5.1)
Если выполняются условия (1), то говорят, что последовательность (хn)сходится к точке а покоординатно.
3необходимости.
Пусть 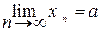 (5.2) в метрическом пространстве Rm.
(5.2) в метрическом пространстве Rm.
Докажем, что выполняются равенства (5.1).
В силу равенства (5.2) по определению предела последовательности в метрическом пространстве Rm будем иметь:
(" e> 0)($N (e))(" n> N) Þ [r (xn, а) < e ],
где r - метрика метрического пространства Rm :
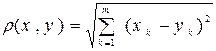 " x, yÎ Rm.
" x, yÎ Rm.
Неравенство r (xn, а) < e примет вид:
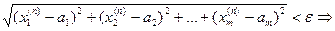


 Þ ½ x1(n)-a1 ½ < e, ½ x2(n)- a2 ½ < e, …, ½ xm(n)-am ½ < e.
Þ ½ x1(n)-a1 ½ < e, ½ x2(n)- a2 ½ < e, …, ½ xm(n)-am ½ < e.
Таким образом, если k = 1, 2, …, m доказано, что
(" e> 0)($N (e))(" n> N) Þ [½ xk(n)- ak ½ < e ]Þ 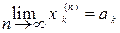 Þ
Þ
равенство (5.1). 4
3достаточности.
Пусть имеют место равенства (5.1).
Докажем, что 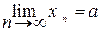 (5.2) в метрическом пространстве Rm.
(5.2) в метрическом пространстве Rm.
Пусть e - произвольное положительное число, в частности пусть его роль играет число 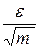 .
.
Поэтому (" e> 0)($nk)(" n> nk) Þ ½ xk(n)-ak ½ < 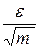 , k = 1, 2, …, m.
, k = 1, 2, …, m.
Выберем число N = max { n1, n2, …, nm }. Тогда " n> N Þ
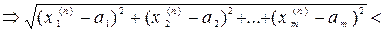
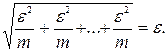
Мы доказали, что(" e> 0)($N (e))(" n> N) Þ [ r (xn, а) < e ]Þ 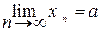 .4
.4
Пример 5.1. Найти предел a = (a1, a2)
последовательности  в пространстве R2.
в пространстве R2.
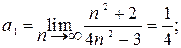
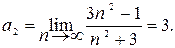
Таким образом, 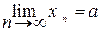 = (1/4; 3).
= (1/4; 3).
Теорема 5.2 (Больцано-Вейерштрасса). Из всякой ограниченной последовательности пространства Rm можно выделить сходящуюся подпоследовательность.
Частный случай этой теоремы для пространства R1 был доказан на первом курсе.
Теорема 5.3. Для того, чтобы последовательность (xn) точек метрического пространства С [ a, b ] с чебышовской метрикой сходилась к элементу х этого пространства, необходимо и достаточно, чтобы функциональная последовательность (xn (t))равномерно сходилась к х (t)на [ a, b ].
Докажем достаточность.
3Напомним, что метрика в пространстве С [ a, b ] имеет вид 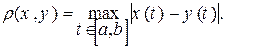
Известно, что функциональная последовательность (xn) равномерно сходится к предельной функции х тогда и только тогда, когда 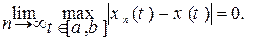
С учетом определения метрики в пространстве С [ a, b ]мы имеем равенство

 по метрике r в метрическом пространстве С [ a, b ]. 4
по метрике r в метрическом пространстве С [ a, b ]. 4
Пример 5.2. xn (t) = tn " tÎ [0; 1/2] Ù " nÎ N. Известно, что на отрезке [0; 1/2] функциональная последовательность xn (t) = tn равномерно сходится к предельной функции x (t) = 0. Таким образом " tÎ [0; 1/2] последовательность (xn) сходится к х = 0 в метрическом пространстве С [0; 1/2].
Теорема 5.4. Если а – предельная точка множества Е метрического пространства (X, r), то существует последовательность (xn), элементы которой принадлежат Е и не равны а, которая сходится к а в этом метрическом пространстве.
Доказательство аналагично доказательству для пространства R.