
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Неопределенного интеграла
|
|
П.1 Определение первообразной функции и
О. Пусть функции 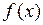 и
и 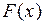 определены на интервале
определены на интервале 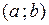 . Функция
. Функция 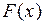 называется первообразной для функции
называется первообразной для функции 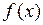 на интервале
на интервале 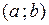 , если
, если 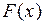 имеет производную на
имеет производную на 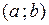 и для
и для 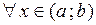 выполняется равенство:
выполняется равенство: 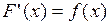 .
.
Задача нахождения функции 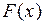 по заданной
по заданной 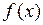 называется задачей неопределенного интегрирования или задачей нахождения первообразной.
называется задачей неопределенного интегрирования или задачей нахождения первообразной.
Понятие первообразной можно ввести и для других промежутков ( ,
, 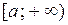 ,
, 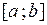 , R). Дадим определение первообразной на отрезке. Если функции
, R). Дадим определение первообразной на отрезке. Если функции 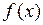 и
и 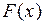 определены на
определены на 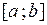 , причем
, причем 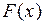 дифференцируема на
дифференцируема на 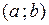 , непрерывна на
, непрерывна на 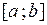 и для
и для 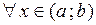
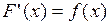 , то функцию
, то функцию 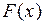 называют первообразной для функции
называют первообразной для функции 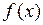 на отрезке
на отрезке 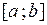 .
.
Утверждение Если 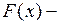 первообразная для функции
первообразная для функции 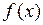 на интервале
на интервале 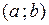 , то функция
, то функция 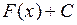 при
при 
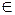 R,
R,  тоже является первообразной для функции
тоже является первообразной для функции 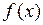 на интервале
на интервале 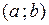 .
.
Справедливо и обратное утверждение.
Теорема Если 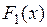 и
и 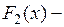 две первообразные для функции
две первообразные для функции 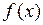 на интервале
на интервале 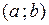 , то для
, то для 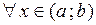 выполняется равенство:
выполняется равенство:
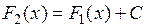 , где
, где  .
.
Доказательство. Обозначим 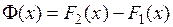 . По определению первообразной, выполняются условия:
. По определению первообразной, выполняются условия: 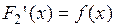 ,
, 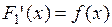 ,
, 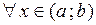 . Отсюда следует, что
. Отсюда следует, что 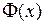 дифференцируема на
дифференцируема на 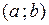 и для
и для 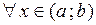
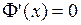 . Согласно следствию из теоремы Лагранжа,
. Согласно следствию из теоремы Лагранжа, 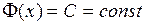 для
для 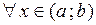 , то есть
, то есть 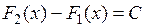 ■
■
О. Неопределенным интегралом от функции 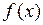 на некотором промежутке
на некотором промежутке  называется совокупность всех первообразных для функции
называется совокупность всех первообразных для функции 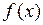 на этом промежутке.
на этом промежутке.
Обозначается символом 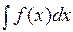 и пишут
и пишут 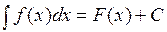 , где
, где 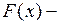 одна из первообразных функции
одна из первообразных функции 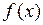 на промежутке
на промежутке 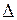 ,
,  .
.
Например,  .
.
Знак 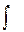 называется знаком интеграла,
называется знаком интеграла, 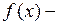 подынтегральной функцией,
подынтегральной функцией, 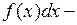 подынтегральным выражением. Его можно также записать в виде
подынтегральным выражением. Его можно также записать в виде 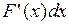 или
или 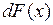 . Т.е.
. Т.е. 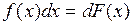 .
.