
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
П.3 Интегрирование иррациональных функций
|
|
Многие интегралы от иррациональных функций удается преобразовать в интегралы от рациональных функций с помощью различных подстановок.
I. Интегралы вида 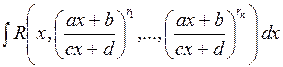 , где
, где 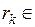 Q,
Q, 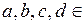 R,
R, 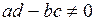 ,
, 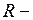 некоторая рациональная функция.
некоторая рациональная функция.
Такие интегралы сводятся к интегралам от рациональных функций с помощью подстановки:
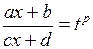 , где
, где 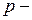 общий знаменатель чисел
общий знаменатель чисел 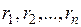 .
.
II. Интегралы вида 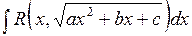 , где
, где 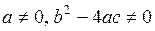 .
.
Такие интегралы сводятся к интегралам от рациональных функций с помощью подстановок Эйлера:
1) 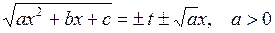 ;
;
2) 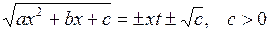 ;
;
3) 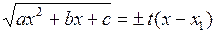 , где
, где 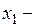 один из корней квадратного трехчлена
один из корней квадратного трехчлена 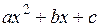 .
.
Подстановки Эйлера обычно приводят к громоздким вычислениям. Поэтому для интегралов вида II иногда применяют другие методы. Например, интегралы вида 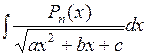 , где
, где 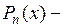 многочлен степени n, следует представить в виде:
многочлен степени n, следует представить в виде:
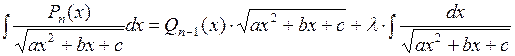 ,
,
где коэффициенты 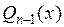 и
и 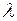 находят методом неопределенных коэффициентов (сначала надо продифференцировать обе части последнего равенства, а затем умножить его на
находят методом неопределенных коэффициентов (сначала надо продифференцировать обе части последнего равенства, а затем умножить его на 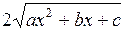 и приравнять коэффициенты при равных степенях
и приравнять коэффициенты при равных степенях 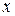 .
.
Интегралы вида 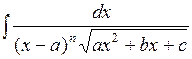 подстановкой
подстановкой 
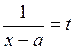 сводятся к интегралам предыдущего вида.
сводятся к интегралам предыдущего вида.
III. Интегралы вида 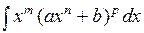 , где
, где 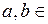 R,
R, 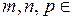 Q,
Q, 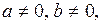
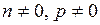 называются интегралами от дифференциального бинома.
называются интегралами от дифференциального бинома.
Такие интегралы сводятся к интегралам от рациональных функций подстановками в трех случаях:
1) если 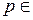 Z, то
Z, то 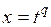 , где
, где 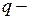 общий знаменатель чисел
общий знаменатель чисел  и
и 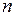 ;
;
2) если 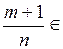 Z, то
Z, то 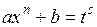 , где
, где 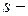 знаменатель числа
знаменатель числа 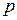 ;
;
3) если 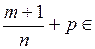 Z, то
Z, то 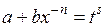 , где
, где 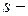 знаменатель числа
знаменатель числа 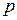 .
.