П.3 Некоторые методы интегрирования

1. Метод замены переменой (метод подстановки).

Пусть дана функция 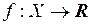, пусть 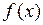имеет первообразную, т.е. 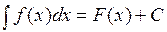, и пусть дана функция , причем дифференцируема. Тогда

или .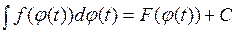

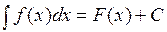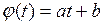Пусть . Возьмем в качестве линейную функцию . Тогда 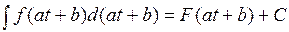. Отсюда

.

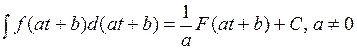Примеры 1) ,

2) .

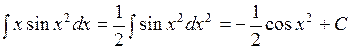2. Метод интегрирования по частям.

Пусть функции и 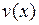имеют непрерывные производные на некотором промежутке. Тогда функция также имеет непрерывную производную на этом промежутке, причем 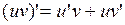. Тогда 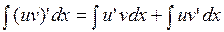. Отсюда 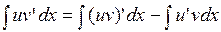или . Отсюда

.

Последняя формула называется формулой интегрирования по частям.

Примеры 1) ,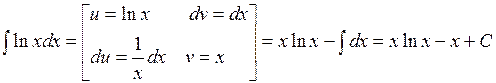

2) .

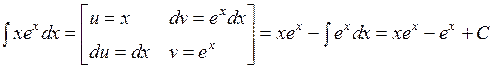Аналогично вычисляются интегралы , где 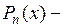некоторый многочлен, 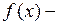одна из функций 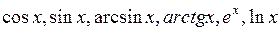и т.п.

Таблица простейших интегралов

,

,

,

,

,

,

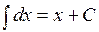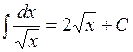
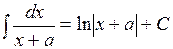
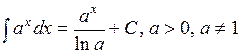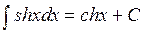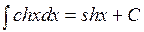
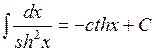
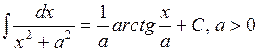
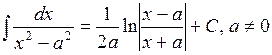
Примеры 1) ;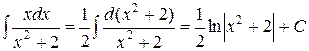

2) ;

3) ;

4) .

Интегрирование функций специального

Вида