Керування точністю та складністю алгоритму кластеризації

Практичні класи задач кластеризації даних є часозалежними завдяки об’ємам даних і складності алгоритму, щоб досягти відповідних характеристик класифікації. Для скорочення втрати часу одночасно задовольняючи вимоги точності, пропонуємо, подібний але простіший за розглянутий [114].

Об’єднання двох кластерів відбувається, якщо функція для них приймає мінімальне значення:

F* = min (F_{k j}), k, j Î I, (2.18)

де I – множина всіх можливих пар початкових об’єктів, кластерів та їх комбінацій.

Прискорення алгоритму полягає в тому, щоб на кожному кроці об’єднувались ті пари об’єктів, критерії яких задовольняють умові:

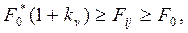(2.19)

де F₀ – найкраще значення функції критерію на даному кроці об'єднання,
k_v (k_v < 1) – коефіцієнт кількості об’єднань на кроці або коефіцієнт швидкості та точності кластеризації.

На рис. 2.2 зображено орієнтовні залежності складності та точності від коефіцієнта швидкості: A.C. – алгоритмічна складність, A.A. – точність алгоритму.

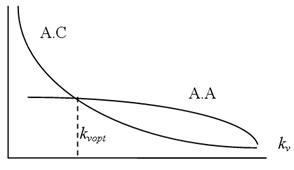
Рис. 2.2. Складність та точність за коефіцієнтом швидкості

Задача полягає в знаходженні найкращого значення коефіцієнту швидкості k_vopt, яке можна використати в алгоритмі для конкретної вибірки даних.

Найкраще значення коефіцієнту k_vopt таке, для якого алгоритмічна складність приймає значення, менше ніж складність обчислення точного варіанту, а точність алгоритму не має втрат. За цим коефіцієнтом результуючі кластери є ті ж, що і при точній кластеризації з параметром k_v = 0.

Рис. 2.3 демонструє характер зміни функції подібності (а) та питомої дисперсії (б) під час процесу кластеризаціїї для значень коефіцієнту k_v: 0, 0.5%, 0.75%, 1%, 5%, 10%, 25% за рівнями дерева згортання.

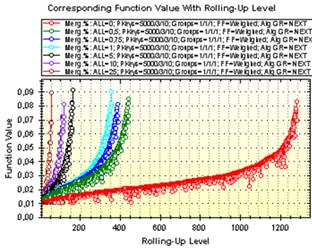
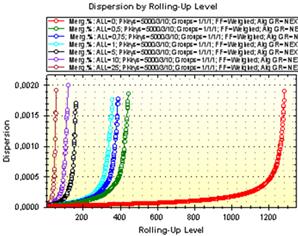
а б

Рис. 2.3. Функція відстані та питомої дисперсії за рівнями дерева згортання

Рис. 2.6 ілюструє залежність характеристики питомого об’єму (a) та зміну питомої густини (б) під час процесу згортання.